题目内容
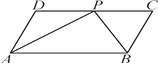
【题目】如图1，在数轴上A、B两点对应的数分别是6，-6，∠DCE=90°（C与O重合，D点在数轴的正半轴上）
（1）如图1，若CF平分∠ACE，则∠AOF=_______;
（2）如图2，将∠DCE沿数轴的正半轴向右平移t（0<t<3）个单位后，再绕顶点C逆时针旋转30t度，作CF平分∠ACE，此时记∠DCF=α.
①当t=1时，α=_________;
②猜想∠BCE和α的数量关系，并证明；
（3）如图3，开始∠D1C1E1与∠DCE重合，将∠DCE沿数轴正半轴向右平移t（0<t<3）个单位，再绕顶点C逆时针旋转30t度，作CF平分∠ACE，此时记∠DCF=α，与此同时，将∠D1C1E1沿数轴的负半轴向左平移t（0<t<3）个单位，再绕顶点C1顺时针旋转30t度，作C1F1平分∠AC1E1,记∠D1C1F1=β，若α，β满足|α-β|=45°，请用t的式子表示α、β并直接写出t的值.
【答案】（1）45°；（2）①30°；②∠BCE=2α，证明见解析；（3）α=45-15t ，β=45+15t，
【解析】
（1）根据角平分线的定义即可得出答案；
（2）①首先由旋转得到∠ACE=120°，再由角平分线的定义求出∠ACF，再减去旋转角度即可得到∠DCF；
②先由补角的定义表示出∠BCE，再根据旋转和角平分线的定义表示出∠DCF，即可得出两者的数量关系；
（3）根据α=∠FCA-∠DCA，β=∠AC1D1+∠AC1F1，可得到表达式，再根据|α-β|=45°建立方程求解.
（1）∵∠ACE=90°，CF平分∠ACE
∴∠AOF=
∠ACE=45°
故答案为：45°；
（2）①当t=1时，旋转角度为30°
∴∠ACE=90°+30°=120°
∵CF平分∠ACE
∴∠ACF=60°，α=∠DCF=∠ACF-30°=30°
故答案为：30°；
②∠BCE=2α，证明如下：
旋转30t度后，∠ACE=(90+30t)度
∴∠BCE=180-(90+30t)=(90-30t)度
∵CF平分∠ACE
∴∠ACF=∠ACE=(45+15t)度
∠DCF=∠ACF-30t=(45-15t)度
∴2∠DCF=2(45-15t)= 90-30t=∠BCE
即∠BCE=2α
（3）α=∠FCA-∠DCA=(90+30t)-30t=45-15t
β=∠AC1D1+∠AC1F1=30t+(90-30t)=45+15t
|30t|=45°
∴
