题目内容
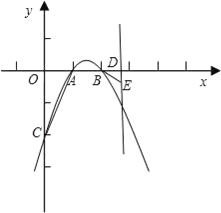
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,﹣2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);
(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.
【答案】(1)二次函数的解析式为y=﹣x2+3x﹣2;
(2)E点坐标为E1(m, ![]() ),E2(m,4﹣2m);
),E2(m,4﹣2m);
(3)F点的坐标为:F1(![]() ,﹣
,﹣![]() ),F2(4,﹣6).
),F2(4,﹣6).
【解析】试题分析:
(1)已知抛物线经过三个点,则可设抛物线的解析式为一般式![]() ,再将三个点的坐标代入到一般式中,得到三元一次方程组即可求解;
,再将三个点的坐标代入到一般式中,得到三元一次方程组即可求解;
(2)△AOC与△BDE都是直角三角形,除直角外,其它的对应关系不确定,所以应分两类讨论,由相似三角形的对应边成比例求出E点的坐标;
(3)A,B是两个确定的点,E点的坐标中含有m也可看作是确定的点,则可根据三个点的坐标,确定第四个点F的坐标,而点F在抛物线上,把F点的坐标代入到抛物线中得到关于m的方程,则可求出点F的坐标.
解:(1)将点A(1,0),B(2,0),C(0,﹣2)代入二次函数y=ax2+bx+c中,得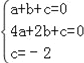
解得a=﹣1,b=3,c=﹣2.
∴y=﹣x2+3x﹣2.(2分)
(2)∵AO=1,CO=2,BD=m﹣2,
当△EDB∽△AOC时,得![]() =
=![]() ,
,
即![]() =
=![]() ,解得ED=
,解得ED=![]() ,
,
∵点E在第四象限,
∴E1(m,![]() ),
),
当△BDE∽△AOC时,![]() =
=![]() 时,即
时,即![]() =
=![]() ,
,
解得ED=2m﹣4,
∵点E在第四象限,
∴E2(m,4﹣2m);
所以有E1(m,![]() ),E2(m,4﹣2m).
),E2(m,4﹣2m).
(3)假设抛物线上存在一点F,使得四边形ABEF为平行四边形,则
EF=AB=1,点F的横坐标为m﹣1,
当点E1的坐标为(m,![]() )时,点F1的坐标为(m﹣1,
)时,点F1的坐标为(m﹣1,![]() ),
),
∵点F1在抛物线的图象上,
∴![]() =﹣(m﹣1)2+3(m﹣1)﹣2,
=﹣(m﹣1)2+3(m﹣1)﹣2,
∴2m2﹣11m+14=0,
∴(2m﹣7)(m﹣2)=0,
∴m=![]() ,m=2(舍去),
,m=2(舍去),
∴F1(![]() ,﹣
,﹣![]() ),
),
当点E2的坐标为(m,4﹣2m)时,点F2的坐标为(m﹣1,4﹣2m),
∵点F2在抛物线的图象上,
∴4﹣2m=﹣(m﹣1)2+3(m﹣1)﹣2,
∴m2﹣7m+10=0,
∴(m﹣2)(m﹣5)=0,∴m=2(舍去),m=5,
∴F2(4,﹣6).
所以F1(![]() ,﹣
,﹣![]() ),F2(4,﹣6).
),F2(4,﹣6).