题目内容
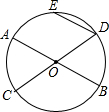
如图,直线AB经过⊙O的圆心O,且与⊙O交于A、B两点,AB=4,半径OC的延长线与过点B的直线交于点D,OC=CD,BC=
OD.点Q为⊙O上一动点.
(1)若∠BCQ=45°,求弦CQ的长.
(2)在点Q运动的过程中,CQ的与直线AB相交于点P,问PO为何值时,△BCQ是等腰三角形;
(3)当Q点运动时,是否存在点P,使得QP=QO?若存在,满足条件的点有几个?并求出相应的∠BCP;若不存在,请说明理由.

| 1 |
| 2 |
(1)若∠BCQ=45°,求弦CQ的长.
(2)在点Q运动的过程中,CQ的与直线AB相交于点P,问PO为何值时,△BCQ是等腰三角形;
(3)当Q点运动时,是否存在点P,使得QP=QO?若存在,满足条件的点有几个?并求出相应的∠BCP;若不存在,请说明理由.

(1)如图,过B作BH⊥CQ,Q为垂足,
∵OC=CD,BC=
OD.
∴△OCB为等边三角形,BC=2,
∴∠COB=60°,
∴∠CQP=30°,
在Rt△BCH中,∠QCB=45°,
∴CH=BH=2×
=
,
在Rt△BQH中,HQ=
BH=
,
∴CQ=CH+QH=
+
;
(2)当BC为腰时,如图,
∴OB垂直平分CQ,
∴PO=1(P点在点O右边);
当BC为底时(如图),
过Q作BC的垂线必过圆心O,过C作CM⊥OB,M为垂足,
∵∠CQB=
∠COB=30°,
∴∠QCB=75°,
∴∠PCM=75°-30°=45°,
∴△CPM为等腰直角三角形,
∴PO=PM-OM=
-1;
(3)当P在OB之间时,∠BCP=40°;
当P在O点左边时(如图),∠BCP=100度.
当P点在B点右侧,如图,∵OQ=PQ,
∴∠QOP=∠P,
∴∠CQO=2∠P,
∴∠OCP=2∠P,
∴∠P=40°,
∴∠BCP=20°.

∵OC=CD,BC=
| 1 |
| 2 |
∴△OCB为等边三角形,BC=2,
∴∠COB=60°,

∴∠CQP=30°,
在Rt△BCH中,∠QCB=45°,
∴CH=BH=2×
| 1 | ||
|
| 2 |
在Rt△BQH中,HQ=
| 3 |
| 6 |
∴CQ=CH+QH=
| 2 |
| 6 |
(2)当BC为腰时,如图,
∴OB垂直平分CQ,
∴PO=1(P点在点O右边);

当BC为底时(如图),
过Q作BC的垂线必过圆心O,过C作CM⊥OB,M为垂足,
∵∠CQB=
| 1 |
| 2 |
∴∠QCB=75°,
∴∠PCM=75°-30°=45°,
∴△CPM为等腰直角三角形,

∴PO=PM-OM=
| 3 |
(3)当P在OB之间时,∠BCP=40°;
当P在O点左边时(如图),∠BCP=100度.

当P点在B点右侧,如图,∵OQ=PQ,
∴∠QOP=∠P,
∴∠CQO=2∠P,
∴∠OCP=2∠P,
∴∠P=40°,
∴∠BCP=20°.


练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目