题目内容
已知,m是方程x2-3x-1=0的一个根,求证: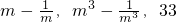 长度的三条线段不能构成三角形.
长度的三条线段不能构成三角形.
解:∵m是方程x2-3x-1=0的一个根,
∴m2-3m-1=0,
∴m=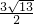 ,
,
∵m>0,
∴m=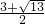 ,
,
∴m-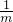 =
=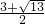 -
- =3,m3-
=3,m3- =(m-
=(m-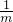 )(m2+1+
)(m2+1+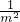 )=3[(m-
)=3[(m-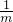 )2+3]=3×(9+3)=36,
)2+3]=3×(9+3)=36,
∵3+33=36,
∴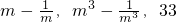 长度的三条线段不能构成三角形.
长度的三条线段不能构成三角形.
分析:首先由m是方程x2-3x-1=0的一个根,求得m的值,再将m代入m-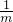 与m3-
与m3- 求解,比较三边关系即可证得结论.注意m3-
求解,比较三边关系即可证得结论.注意m3- =(m-
=(m-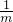 )[(m-
)[(m-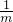 )2+3].
)2+3].
点评:此题考查了方程解的定义,一元二次方程的解法以及立方公式与完全平方公式的知识.注意整体思想的应用是解此题的关键.
∴m2-3m-1=0,
∴m=
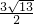 ,
,∵m>0,
∴m=
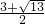 ,
,∴m-
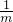 =
=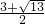 -
- =3,m3-
=3,m3- =(m-
=(m-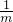 )(m2+1+
)(m2+1+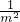 )=3[(m-
)=3[(m-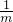 )2+3]=3×(9+3)=36,
)2+3]=3×(9+3)=36,∵3+33=36,
∴
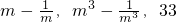 长度的三条线段不能构成三角形.
长度的三条线段不能构成三角形.分析:首先由m是方程x2-3x-1=0的一个根,求得m的值,再将m代入m-
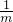 与m3-
与m3- 求解,比较三边关系即可证得结论.注意m3-
求解,比较三边关系即可证得结论.注意m3- =(m-
=(m-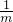 )[(m-
)[(m-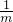 )2+3].
)2+3].点评:此题考查了方程解的定义,一元二次方程的解法以及立方公式与完全平方公式的知识.注意整体思想的应用是解此题的关键.

练习册系列答案
相关题目