题目内容
【题目】在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.
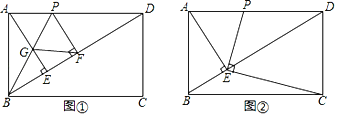
(1)若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;
(2)若PE⊥EC,如图②,求证:AEAB=DEAP;
(3)在(2)的条件下,若AB=1,BC=2,求AP的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)想办法证明AG=PF,AG∥PF,推出四边形AGFP是平行四边形,再证明PA=PF即可解决问题.
(2)证明△AEP∽△DEC,可得 ![]() ,由此即可解决问题.
,由此即可解决问题.
(3)利用(2)中结论.求出DE,AE即可.
(1)证明:如图①中,
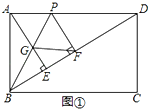
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AE⊥BD,
∴∠AED=90°,
∴∠BAE+∠EAD=90°,∠EAD+∠ADE=90°,
∴∠BAE=∠ADE,
∵∠AGP=∠BAG+∠ABG,∠APD=∠ADE+∠PBD,∠ABG=∠PBD,
∴∠AGP=∠APG,
∴AP=AG,
∵PA⊥AB,PF⊥BD,BP平分∠ABD,
∴PA=PF,
∴PF=AG,
∵AE⊥BD,PF⊥BD,
∴PF∥AG,
∴四边形AGFP是平行四边形,
∵PA=PF,
∴四边形AGFP是菱形.
(2)证明:如图②中,
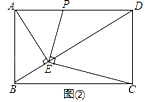
∵AE⊥BD,PE⊥EC,
∴∠AED=∠PEC=90°,
∴∠AEP=∠DEC,
∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,
∴∠EAP=∠EDC,
∴△AEP∽△DEC,
∴![]() ,
,
∵AB=CD,
∴AEAB=DEAP;
(3)解:∵四边形ABCD是矩形,
∴BC=AD=2,∠BAD=90°,
∴BD=![]() ,
,
∵AE⊥BD,
∴S△ABD=![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE=![]()
∴DE=![]() ,
,
∵AEAB=DEAP
∴AP=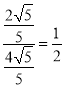 .
.

练习册系列答案
相关题目