题目内容
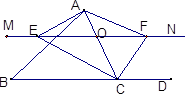
如图,已知四边形ABCD是平行四边形.
(1)求证:△MEF∽△MBA;
(2)若AF、BE分别是∠DAB,∠CBA的平分线,求证:DF=EC.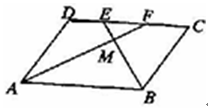
(1)求证:△MEF∽△MBA;
(2)若AF、BE分别是∠DAB,∠CBA的平分线,求证:DF=EC.

(1)根据平行四边形的性质可得∠EFM=∠MAB,∠FEM=∠MBA,即可证得结论;
(2)由AB∥CD可得∠DFA=∠FAB,再结合角平分线的性质可得∠DAF=∠DFA,从而证得结论.
(2)由AB∥CD可得∠DFA=∠FAB,再结合角平分线的性质可得∠DAF=∠DFA,从而证得结论.
试题分析:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EFM=∠MAB,∠FEM=∠MBA,
∴△MEF∽△MBA;
(2)∵AB∥CD,
∴∠DFA=∠FAB,
∵AF、BE分别是∠DAB,∠CBA的平分线,
∴∠DAF=∠FAB,
∴∠DAF=∠DFA,
∴DA=DF,
同理得出CE=CB,
∴DF=EC.
点评:平行四边形的性质是初中数学的重点,是中考中极为常见的知识点,非常基础,需熟练掌握.

练习册系列答案
相关题目
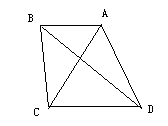

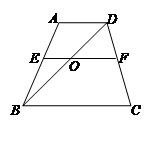
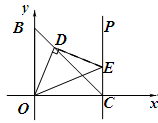
 中,
中,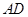 ∥
∥ ,
, ,
, ,
, ,
,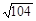 =
=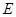 在
在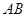 上,
上,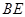 =4.
=4.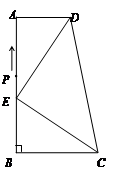
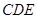 的形状,并说明理由;
的形状,并说明理由;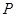 在线段
在线段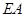 上从点
上从点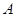 移动,设移动时间为
移动,设移动时间为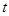 秒(
秒( 为直角三角形?若存在直接写出
为直角三角形?若存在直接写出