Question

（9分）在平面直角坐标系xOy中，点B(0，3)，点C是x轴正半轴上一点，连结BC，过点C作直线CP∥y轴.

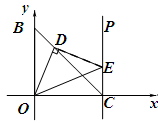
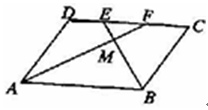
（1）若含45°角的直角三角形如图所示放置．其中，一个顶点与点O重合，直角顶点D在线段BC上，另一个顶点E在CP上．求点C的坐标；
（2）若含30°角的直角三角形一个顶点与点O重合，直角顶点D在线段BC上，另一个顶点E在CP上，求点C的坐标．

Answer 1

(1) C(3，0) ,（2）（，0） (3,0).

试题分析：由题意知，求C点坐标很难，所以要做辅助线，结合平面直角坐标系的性质求得，在（2）中由已知得有两种情况，解：（1）过点D分别作DG⊥x轴于G，
DH⊥PC于H.   1分；

∴，
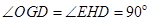∵△ODE是等腰直角三角形，
∴OD=DE，，
∵CP∥y轴，
∴四边形DGCH是矩形，     2分；
∴，DH=GC.
∴，
∴，
∴△ODG≌△EDH.          3分；
∴DG=DH.
∴DG=GC，
∴△DGC是等腰直角三角形，
∴，      4分；
∴tan，
∴OC=OB="3."
∴点C的坐标为（3,0）     5分；
分两种情况：
当时，
过点D分别作DG⊥x轴于G，
DH⊥PC于H.  

∴，
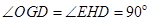∵△ODE是直角三角形，
∴tan，
，
∵CP∥y轴，
∴四边形DGCH是矩形，
∴，DH=GC.
∴，
∴，
∴△ODG∽△EDH.         6分；
∴.
∴，
∴tan，
∴，
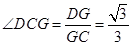∴tan，
∴OC=.           7分；
当时，
过点D分别作DG⊥x轴于G，
DH⊥PC于H.  

∴，
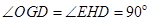∵△ODE是直角三角形，
∴tan，
，
∵CP∥y轴，
∴四边形DGCH是矩形，
∴，DH=GC.
∴，
∴，
∴△ODG∽△EDH.        8分；
∴.
∴，
∴tan，
∴，
∴tan，
∴OC=.         9分.
∴点C的坐标为（,0）、（,0）.
点评：熟练掌握以上各定义性质，在解题时要结合已知所给的条件，在做辅助线的情况下，可求得，第二问求之值时，容易遗漏，需注意，本题涉及到的知识面广，计算量教大，也容易出错。综合性很强，属于难题。