Question

【题目】已知一次函数y=﹣ x+6的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．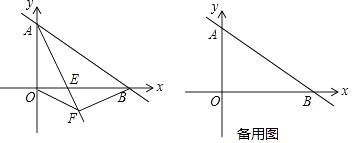

（1）求点B的坐标；
（2）求直线AE的表达式；
（3）过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．

Answer 1

【答案】
（1）解：当y=﹣ x+6=0时，x=8，

∴点B的坐标为（8，0）．

（2）解：当x=0时，y=﹣ x+6=6，

∴点A的坐标为（0，6），

∴OA=6，OB=8，

∴AB= =10．

∵AE平分∠BAO，交x轴于点E，

∴ = ，

∴OE= BE．

∵OE+BE=OB=8，

∴OE=3，BE=5，

∴点E的坐标为（3，0）．

设直线AE的表达式为y=kx+b，

将A（0，6）、E（3，0）代入y=kx+b，

，解得： ，

∴直线AE的表达式为y=﹣2x+6．

（3）解：过点F作FG⊥x轴于点G，如图所示．

∵BF⊥AE，

∴∠BFE=90°=∠AOE．

∵∠AEO=∠BEF，

∴△AOE∽△BFE，

∴ = = ．

∵OA=6，OE=3，

∴AE=3 ．

∵BE=5，

∴BF=2 ，EF= ．

同理可得：△BEF∽△BFG，

∴BG=4，FG=2．

∵OB=8，

∴OG=4=BG，

∴△OFB为等腰三角形，

∴S△OFB= OBFG=8．

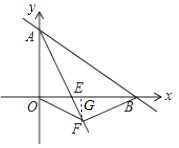
【解析】（1）将y=0代入直线AB的表达式中求出x值，此题得解；（2）利用一次函数图象上点的坐标特征求出点A的坐标，结合勾股定理可求出AB的长度，再利用角平分线的性质即可求出点E的坐标，根据点A、E的坐标利用待定系数法即可求出直线AE的表达式；（3）过点F作FG⊥x轴于点G，由BF⊥AE可得出△AOE∽△BFE，根据相似三角形的性质可得出BF、EF的长度，同理可得出△BEF∽△BFG，根据相似三角形的性质可得出BG、FG的长度，结合OB=8即可得出OG=BG，由此可得出△OFB为等腰三角形，再根据三角形的面积公式可得出△OFB的面积．
【考点精析】掌握相似三角形的性质是解答本题的根本，需要知道对应角相等，对应边成比例的两个三角形叫做相似三角形．