题目内容
如图，等腰梯形 ABCD中，AB∥DC，BD平分∠ABC，∠DAB=60°，若梯形周长为40cm，则AD= ．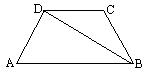
8cm
试题分析：解：因为等腰梯形ABCD中，∠CBA=∠DAB=60°因为BD平分∠ABC，
∴∠ABD=∠DBC=30°，
因为AB∥DC∴∠CBD=∠CDB=30°，所以CD=CB。
∠C+∠CBA=180°，所以∠C=120°。则∠CDA=∠C=120°。∠ADB=120°-∠CDB=90°。
所以BD⊥CD，且∠DBA=30°
∴BC=2CD，所以梯形ABCD周长=CD+AD+BC+AB=5AD
所以5AD=40，
∴AD=8cm
点评：此题主要考查学生对等腰梯形的性质的理解及运用．根据已知可推出BC=2CD，根据周长公式可求得腰长及高的长，再根据面积公式即可求得其面积．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
（
），∠GEF的两边分别交矩形的边于点M，点N．当△MEN为等腰三角形时，求此时△MEN的面积．
的角平分线AF和梯形的高BG(保留作图痕迹，不写作法和证明)；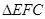
的面积为 ．
