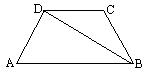
题目内容
如图,四边形ABCD是平行四边形,AB=2,以边AB为直径的⊙O经过点D,且∠DAB=45°.

(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若以C为圆心的⊙C与⊙O 相切,求⊙C的半径.

(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若以C为圆心的⊙C与⊙O 相切,求⊙C的半径.
(1)直线CD与⊙O相切;(2)-1或+1
试题分析:(1)连接OD,根据平行四边形的性质可得AB//CD,即得∠DAB+∠ADC=180°,从而可以求得∠ADC的度数,再根据圆的基本性质求解即可;
(2)作CE⊥OB,交OB的延长线于点E,连接OC,根据平行四边形的性质可得AD//BC,即得∠CBE=∠DAB=45°,则可得BE=CE=1,在Rt△OCE中,根据勾股定理可求得OC的长,即可求得结果.
(1)直线CD与⊙O相切.
连接OD
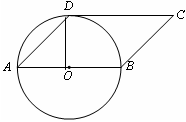
∵四边形ABCD是平行四边形,
∴AB//CD.
∴∠DAB+∠ADC=180°.
∵∠DAB=45°,
∴∠ADC=135°.
∵OA=OD,
∴∠ODA=∠DAO=45°.
∴∠ODC=∠ADC-∠ODA=90°
∴OD⊥CD,
∵OD为⊙O半径,
∴直线CD与⊙O相切;
(2)作CE⊥OB,交OB的延长线于点E,连接OC
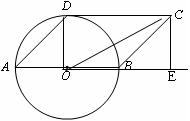
∵四边形ABCD是平行四边形,
∴AD//BC.
∴∠CBE=∠DAB=45°.
∴BE=CE=1.
在Rt△OCE中,OC==
∵⊙C与⊙O 相切,
∴⊙C的半径为-1或+1.
点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
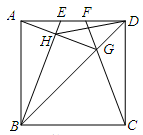
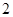 的正方形的中心
的正方形的中心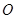 为端点,引两条相互垂直的射线,分别与正方形的两邻边交于
为端点,引两条相互垂直的射线,分别与正方形的两邻边交于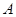 、
、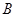 两点,则线段
两点,则线段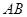 的最小值是 .
的最小值是 .