Question

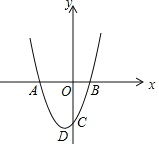
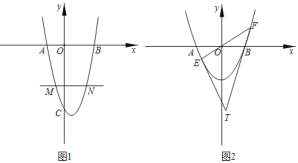
【题目】如图1，抛物线y＝a（x﹣h）2﹣9交x轴于A、B两点，交y轴于点C．

（1）若A（﹣2，0），当h＝1时，

①求抛物线的解析式．

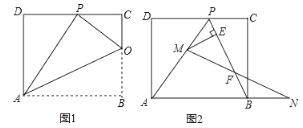
②平行x轴的直线y＝t交抛物线于M、N点（点M在点N左侧），过M、N、C三点作⊙P．若MP⊥CP，求t值．

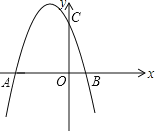
（2）如图2，当h＝0时，正比例函数y＝kx交抛物线于E、F两点，直线AE、BF相交于T点，求点T的运动轨迹．

Answer 1

【答案】（1）①；②；（2）T在直线上运动．

【解析】

（1）①由已知可得，将A（-2，0）代入抛物线解析式可得；

②由已知可得P点在MN的垂直平分线上，P点在抛物线对称轴x=1上，设

，则△PCM是等腰直角三角形，所以，，∠MNC=∠MPC=45°，设MN与y轴的交点为H，则HN=HC，所以，令，可得，，求出t即可；

（2）由已知可得y=ax2-9，设A（-s，0），B（s，0），所以as2=9，AE的直线解析式为y=k1x+k1s与抛物线相交可得，，直线BF的解析式为y=k2x-k2s与抛物线相交可得，，直线EF的解析式为y=kx与抛物线相交可得，，，，，直线AE与直线BF相交可得T，，求得T，，可得T在直线y=18上运动．

（1）①将h=1，A(﹣2，0)代入得：

解得：,

∴

即：；

②∵M、N、C三点作⊙P，

∴P点在MN的垂直平分线上，

∴P点在抛物线对称轴x=1上，

如图，MN交y轴和抛物线对称轴于分别为点H和G，过点C作抛物线对称轴x=1的垂线垂足为D，连接NC，

∵MN平行x轴，

∴四边形CDGH为矩形，

∴DG=HC，GH=CD=1，

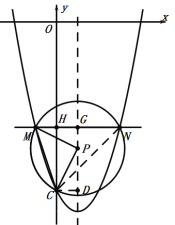
∵PM=PC，PM⊥PC，

∴△PCM是等腰直角三角形，∠MPC=∠MGP=∠PDC=，

∵∠MPG+∠CPD=∠PCD+∠CPD =，

∴∠MPG=∠PCD，

在和中，，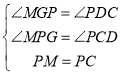

∴，

∴，，

设，

∴，

∴，

∴m=﹣t﹣6，

∴∠MNC=∠MPC=45°，

∴HN=HC，

∴，

∴，

令，

∴，

∴，

∴(舍)或，

∴；

(2)∵，

∴，

设，

∴，

∴AE的直线解析式为，

∴，

∴，，

直线BF的解析式为，

∴，

∴，，

∵直线EF的解析式为，

∴，

∴，，

∵as2=9，

∴，，

∴，

∵，

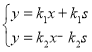∴T，)，

∵，

∴T，)，

∴T在直线y=18上运动．