题目内容
【题目】阅读以下短文,然后解决下列问题:
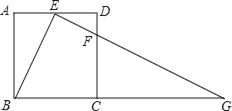
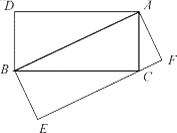
如果一个三角形和一个矩形满足条件:三角形的一边与矩形的一边重合,且三角形的这边所对的顶点在矩形这边的对边上,则称这样的矩形为三角形的“友好矩形”. 如图①所示,矩形ABEF即为△ABC的“友好矩形”. 显然,当△ABC是钝角三角形时,其“友好矩形”只有一个 .
(1) 仿照以上叙述,说明什么是一个三角形的“友好平行四边形”;
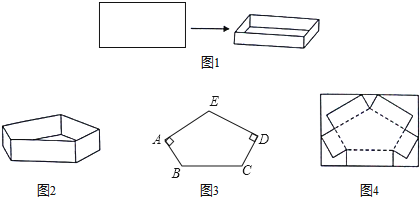
(2) 如图②,若△ABC为直角三角形,且∠C=90°,在图②中画出△ABC的所有“友好矩形”,并比较这些矩形面积的大小;
(3) 若△ABC是锐角三角形,且BC>AC>AB,在图③中画出△ABC的所有“友好矩形”,指出其中周长最小的矩形并加以证明.

【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)类似“友好矩形”的定义,即可写出“友好平行四边形”的定义:如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”;
(2)根据定义,则分别让直角三角形的直角边或斜边当矩形的一边,过第三个顶点作它的对边,从而画出矩形.根据每个矩形和直角三角形的面积的关系,比较两个矩形的面积大小;
(3)分别以三角形的一边当矩形的另一边,过第三个顶点作矩形的对边,从而画出矩形,根据三角形和矩形的面积公式,可知三个矩形的面积相等,设矩形的面积是S,三角形的三条边分别是a,b,c.根据矩形的面积由其中一边表示出矩形的另一边,进一步求得其周长,运用求差法比较它们的周长的大小.
(1) 如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的对边上,则称这样的平行四边形为三角形的“友好平行四边形”.
(2) 此时共有2个友好矩形,如图的矩形BCAD、矩形ABEF.
易知,矩形BCAD、ABEF的面积都等于△ABC面积的2倍,∴ △ABC的“友好矩形”的面积相等.
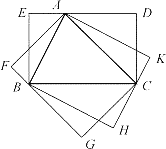
(3) 此时共有3个友好矩形,如图的BCDE、CAFG及ABHK,其中的矩形ABHK的周长最小 .
证明如下:易知,这三个矩形的面积相等,令其为S. 设矩形BCDE、CAFG及ABHK的周长分别为L1,L2,L3,△ABC的边长BC=a,CA=b,AB=c,则L1=![]() +2a,L2=
+2a,L2=![]() +2b,L3=
+2b,L3=![]() +2c .
+2c .
∴ L1- L2=(![]() +2a)-(
+2a)-(![]() +2b)=2(a-b)
+2b)=2(a-b)![]() ,而 ab>S,a>b,
,而 ab>S,a>b,
∴ L1- L2>0,即L1> L2 . 同理可得,L2> L3 .
∴ L3最小,即矩形ABHK的周长最小.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案