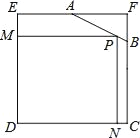
题目内容
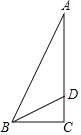
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.
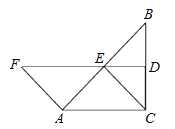
(1)说明四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.
【答案】(1)说明见解析;(2)当∠B=30°时,四边形ACEF是菱形.理由见解析.
【解析】
试题(1)证明△AEC≌△EAF,即可得到EF=CA,根据两组对边分别相等的四边形是平行四边形即可判断;
(2)当∠B=30°时,四边形ACEF是菱形.根据直角三角形的性质,即可证得AC=EC,根据菱形的定义即可判断.
(1)证明:由题意知∠FDC=∠DCA=90°,
∴EF∥CA,
∴∠FEA=∠CAE,
∵AF=CE=AE,
∴∠F=∠FEA=∠CAE=∠ECA.
在△AEC和△EAF中,
∵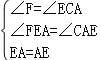
∴△EAF≌△AEC(AAS),
∴EF=CA,
∴四边形ACEF是平行四边形.
(2)解:当∠B=30°时,四边形ACEF是菱形.
理由如下:∵∠B=30°,∠ACB=90°,
∴AC=![]() AB,
AB,
∵DE垂直平分BC,
∴∠BDE=90°
∴∠BDE=∠ACB
∴ED∥AC
又∵BD=DC
∴DE是△ABC的中位线,
∴E是AB的中点,
∴BE=CE=AE,
又∵AE=CE,
∴AE=CE=![]() AB,
AB,
又∵AC=![]() AB,
AB,
∴AC=CE,
∴四边形ACEF是菱形.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目