��Ŀ����
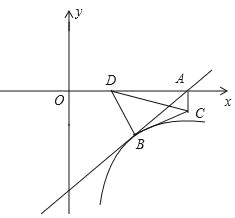
����Ŀ��ij��λΪ����Ӧ������������ȫ�������ĺ��٣������ڳ��Ϳ��ֱ�Ϊ20m��16m�ľ��δ�������һ��40m2�ľ��ν�����ABCD���ý�����������ǽ�������������ô����ľ�ǽ��(��ͼΪƽ��ʾ��ͼ)����ÿ���ǽ���������õľ�ǽ�ڳ��Ȳ��ó����䳤�ȵ�һ�룬��֪װ��ǽ�ڵķ���Ϊ20Ԫ/m2���½�(��װ��)ǽ�ڵķ���Ϊ80Ԫ/m2���轡������3m��������AB�ij�Ϊxm��BC�ij�Ϊym����������ǽ�ڵ���Ͷ��ΪwԪ��
��1����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��2����w��x�ĺ�����ϵʽ�������������������AB��Ϊ8mʱ��Ͷ��Ϊ����Ԫ��

���𰸡���1��y��![]() ��5��x��10������2��w=300����x+
��5��x��10������2��w=300����x+![]() ������x=8ʱ��w��3900��Ԫ����
������x=8ʱ��w��3900��Ԫ����
��������
��1������ʽ��Լ��Ա���ȡֵ��Χֻ����ݡ������õľ�ǽ�ڳ��Ȳ��ó����䳤�ȵ�һ�롱���������
��2����Ͷ���������ֹ��ɣ���ǽ���½�ǽ��Ӧ�ø��ݣ�1���н���������������ú�x��ʽ�ӷֱ��ʾ������������⣮
�⣺��1�����������֪y��![]() ��
��
��
��5��x��10
��2���������֪w=��x+![]() ����3��80+��x+
����3��80+��x+![]() ����3��20=300����x+
����3��20=300����x+![]() ����
����
��x=8ʱ��w��300(8+![]() )��3900��Ԫ����
)��3900��Ԫ����