题目内容
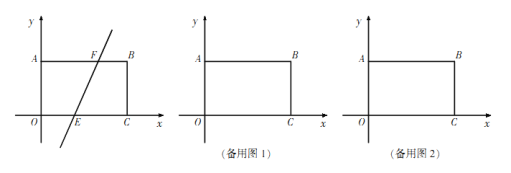
【题目】在平面直角坐标系中,长方形![]() 的边
的边![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 的坐标是(5,3),直线
的坐标是(5,3),直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() .
.
(1)用含![]() 的代数式表示点
的代数式表示点![]() 的坐标;
的坐标;
(2)若![]() ,当
,当![]() 为何值时,
为何值时, ![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,当
,当![]() 平分
平分![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根据B、F两点的纵坐标都是3,即可表示出点F的坐标,对于直线![]() ,令y=0,可表示点E坐标;
,令y=0,可表示点E坐标;
(2)分三种情形:①当 AE=AF时;②当FA=FE时;③ 当EA=EF时分别求解即可;
(3)由AB//OC,C F 平分 ∠EFB,推出∠BFC=∠FCE=∠EFC,推出![]() ,由此构建方程即可解决问题.
,由此构建方程即可解决问题.
解: (1)∵四边形 OABC是矩形,
∴BF//OC
∵B(5,3)
∴点 F的纵坐标为 3
∴3=kx+b
∴![]()
∴ ![]()
对于直线 y=kx+b,令 y=0,得到 ![]()
∴![]()
( 2 ) ∵![]()
∵![]()
![]()
①当AE=AF时,
∴OE=![]() ,AE=AF=
,AE=AF=![]()
∴ ![]()
![]()
∴![]() 或
或![]() (舍去)
(舍去)
∴![]()
② 当FA=FE时,
![]()
![]() 或
或![]() (舍去)
(舍去)
∴ ![]()
③ 当EA=EF时,
AF=2OE =2 ![]()
![]() =
=![]()
![]()
∴ 这种情况不存在
∴![]() 或
或![]() 时,△AEF是等腰三角形。
时,△AEF是等腰三角形。
(3)当![]() 时,如图,连接C F
时,如图,连接C F
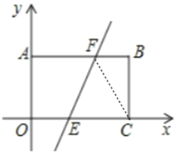
∵AB//OC
C F 平分 ∠EFB
∴∠BFC=∠FCE=∠EFC
∴EF=EC
∴![]()
∵![]() ,
, ![]()
∴ ![]()
∴![]() 或
或![]() (舍去)
(舍去)
∴![]()

练习册系列答案
相关题目
【题目】甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如表,请根据表中数据解答下列问题
进球数/个 | 10 | 9 | 8 | 7 | 6 | 5 |
甲 | 1 | 1 | 1 | 4 | 0 | 3 |
乙 | 0 | 1 | 2 | 5 | 0 | 2 |
(1)分别写出甲、乙两班选手进球数的平均数、中位数与众数;
(2)如果要从这两个班中选出一个班级参加学校的投篮比赛,争取夺得总进球团体的第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?