题目内容
【题目】在
中，
，
的垂直平分线与
所在的直线相交所得到的锐角为
，则
等于______________度．
【答案】65°或25°
【解析】
(1)当△ABC是锐角三角形时，根据题目条件得到∠A=50°，利用△ABC是等腰三角形即可求解；(2)当△ABC是钝角三角形时，同理可得即可得出结果．
解：(1)当△ABC是锐角等腰三角形时，如图1所示
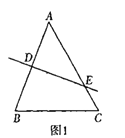
由题知：DE⊥AB，AD=DB，∠AED=40°
∴∠A=180°-90°-40°=50°
∵AB=AC
∴△ABC是等腰三角形
∴∠ABC=∠ACB
∴∠ABC=(180°-50°)÷2=65°
(2)当△ABC是钝角三角形时，如图2所示
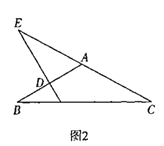
由题知：DE⊥AB，AD=DB，∠AED=40°
∴∠AED+∠ADE=∠BAC
∴∠BAC=90°+40°=130°
∵AB=AC
∴△ABC是等腰三角形
∴∠ABC=∠ACB
∴∠ABC=(180°-130°)÷2=25°
∴∠ABC=65°或25°
故答案为：65°或25°
练习册系列答案
相关题目
