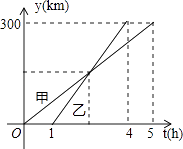
��Ŀ����
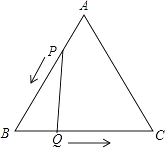
����Ŀ����֪��A��a��0����B��0��b�����㣨a��4��2+|b��6|=0���ֱ����A��B��x�ᡢy��Ĵ��߽��ڵ�C����ͼ����P��ԭ���������ÿ��2����λ���ȵ��ٶ�����O��B��C��A��O��·���ƶ��� 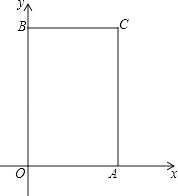
��1��д��A��B��C��������ꣻ
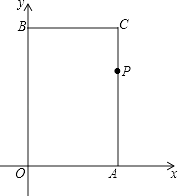
��2������P�ƶ���6��ʱ�������ʱP���λ�ã���д����P��λ�ã�
��3�����ᣨ2����B��P���㣬���߶�BP����ƽ��h����λ��h��0�����õ�B��P�䣬��B��P�佫�ı���OACB���ܳ��ֳ���ȵ������֣���h��ֵ��
���𰸡�
��1���⣺�ɷǸ��������ʵã�a��4=0��b��6=0��
���a=4��b=6��
���ԣ�A��4��0����B��0��6����C��4��6��
��2���⣺��P�˶���·��=2��6=12��
���ԣ���P�ڱ�AC�ϣ�
AP=6+4+6��12=4��
P���λ����ͼ��P��4��4����
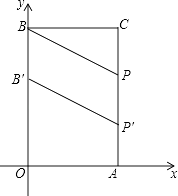
��3���⣺��ͼ����PP��=BB��=h��
��CP��=h+2��AP��=4��h��OB��=6��h��
��B��P�佫�ı���OACB���ܳ��ֳ���ȵ������֣�
��h+4+��h+2��=��6��h��+4+��4��h����
���h=2��
��h��ֵΪ2
����������1�����ݷǸ�����������ʽ���a��b��ֵ��Ȼ��д����A��B�����꣬�ٸ��ݾ��ε�����д����C�����ꣻ��2�������P�˶���·�̣�Ȼ��ȷ������P��AC���ϲ����AP��ֵ����д����P�����꼴�ɣ���3������ƽ�Ƶ����ʺ;��ε����ʱ�ʾ��BB�䡢CP�䡢AP�䡢OB�䣬Ȼ������ܳ��Ķ����г�������⼴�ɣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�