��Ŀ����
����Ŀ����֪����ͼ����ABC�DZ߳�Ϊ4cm�ĵȱ������Σ�����P��Qͬʱ��A��B����������ֱ���AB��BC���������ƶ������ǵ��ٶȶ���1cm/s������P�����Bʱ��P��Q����ֹͣ�˶������P���˶�ʱ��t��s����������и����⣺ 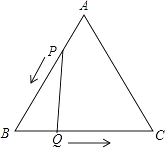
��1�����ABC�������
��2����tΪ��ֵ�ǣ���PBQ��ֱ�������Σ�
��3��̽�����Ƿ����ijһʱ��t��ʹ�ı���APQC������ǡ�ABC����İ˷�֮�壿������ڣ����t��ֵ����������˵�����ɣ�
���𰸡�
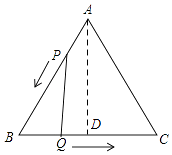
��1���⣺��ͼ������A��AD��BC�����BAC=30�㣬
��AC=4��
��CD= ![]() AC=2��
AC=2��
��Rt��ACD��AD= ![]() =2
=2 ![]() ��
��
���ABC�����= ![]() ��BC��AD=
��BC��AD= ![]() ��4��2
��4��2 ![]() =4
=4 ![]()
��2���⣺�辭��t�룬��PBQ��ֱ�������Σ���AP=tcm��BQ=tcm��
��ABC�У�AB=BC=4cm����B=60�㣬
��BP=��4��t��cm��
����PBQ��ֱ�������Σ�������������
�� ����BQP=90��ʱ��BQ= ![]() BP��
BP��
��t= ![]() ��4��t����
��4��t����
���t= ![]() ���룩��
���룩��
�ڵ���BPQ=90��ʱ��BP= ![]() BQ��
BQ��
4��t= ![]() t��
t��
���t= ![]() ���룩��
���룩��
������������t= ![]() ���
��� ![]() ��ʱ����PBQ��ֱ��������
��ʱ����PBQ��ֱ��������
��3���⣺������������t��
���ɣ���ͼ����QD��AB��D�����BQD=30�㣬

��QD= ![]() BD=
BD= ![]() ��
�� ![]() t=
t= ![]() t��
t��
���BQP�����= ![]() ��BP��QD
��BP��QD
= ![]() ����4��t����
����4��t���� ![]() t
t
= ![]() t��
t�� ![]() t2��
t2��
���ı���APQC������ǡ�ABC����� ![]() ʱ����BQP������ǡ�ABC�����
ʱ����BQP������ǡ�ABC����� ![]() ��
��
�� ![]() t��
t�� ![]() t2=
t2= ![]() ��4
��4 ![]() ��
��
����ã�t2��4t+6=0��
�ߡ�=b2��4ac=16��4��1��6=��8��0��
�����������t��ʹ�ı���APQC������ǡ�ABC����İ˷�֮�壮
����������1������A��AD��BC�����ݹ��ɶ������AD�ij������������ε������ʽ���н�ɣ���2������������������ۣ��١�BPQ=90�㣻�ڡ�BQP=90�㣬Ȼ����ֱ��������BQP�и���BP��BQ�ij��͡�B�Ķ���������⼴�ɣ���3������QD��AB��D�����ݡ�BQD=30�㣬�õ�QD= ![]() BD=
BD= ![]() ��
�� ![]() t=
t= ![]() t��Ȼ������ı���APQC������ǡ�ABC����İ˷�֮�壬�ɵó�һ������t�ķ��̣���������⣬��˵��������������tֵ����������н⣬��ô�����tֵ���ɣ�
t��Ȼ������ı���APQC������ǡ�ABC����İ˷�֮�壬�ɵó�һ������t�ķ��̣���������⣬��˵��������������tֵ����������н⣬��ô�����tֵ���ɣ�
�����㾫����ͨ��������������ʽ�ͺ�30�Ƚǵ�ֱ�������Σ����ո����б�ʽ��=b2-4ac��������Է�Ϊ3�������1������>0ʱ��һԪ���η�����2������ȵ�ʵ����2������=0ʱ��һԪ���η�����2����ͬ��ʵ����3������<0ʱ��һԪ���η���û��ʵ��������ֱ���������У����һ����ǵ���30�㣬��ô�����Ե�ֱ�DZߵ���б�ߵ�һ�뼴���Խ����⣮

 �����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӽݾ��㽭��ѧ������ϵ�д�