题目内容
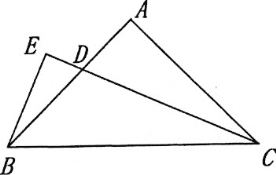
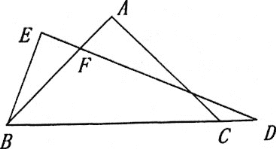
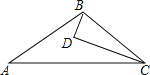
【题目】如图,在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
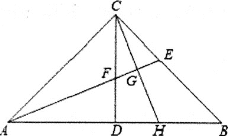
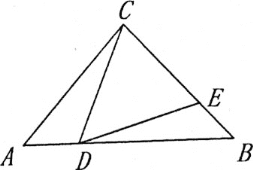
(1)如图,若BC=BD,求证:CD=DE;
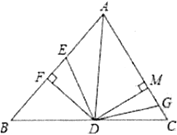
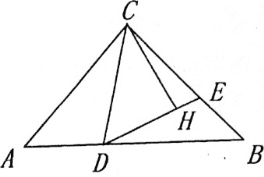
(2)如图,过点C作CH⊥DE,垂足为H,若CD=BD,![]() ,直接写出CE-BE的值为________.
,直接写出CE-BE的值为________.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先根据条件得出∠ACD=∠BDE,BD=AC,再根据ASA判定△ADC≌△BED,即可得到CD=DE;
(2)先根据条件得出∠DCB=∠CDE,进而得到CE=DE,再在DE上取点F,使得FD=BE,进而判定△CDF≌△DBE(SAS),得出CF=DE=CE,再根据CH⊥EF,运用三线合一即可得到FH=HE,最后得出DE-BE=DE-DF=EF=2HE=2.
(1)∵AC=BC,∠CDE=∠A,
∴∠A=∠B=∠CDE,
∠BDC=∠A+∠ACD
∴∠ACD=∠BDE,
又∵BC=BD,
∴BD=AC,
在△ADC和△BED中,
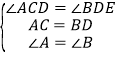
∴△ADC≌△BED(ASA),
∴CD=DE;
(2)![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目