Question

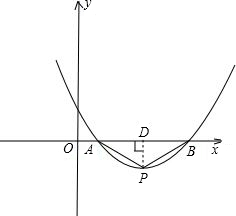
抛物线y=ax²+bx+c与x轴交于A，B两点，P为抛物线的顶点，若∠APB=120°，则b²-4ac=______．

Answer 1

如图，作PD⊥x轴于D，
设A、B点坐标分别为x₁、x₂，
则AB=|x₁-x₂|=

(x1+x2)2-4x1x2

=

(- b a )2-4 c a

=

b2-4ac

|a|

；
抛物线顶点坐标为（-

b

2a

，

4ac-b2

4a

），
则DP的长为|

4ac-b2

4a

|，
∵∠APB=120°，
由抛物线是轴对称图形可知，△APB为等腰三角形，
可知，∠PAD=∠PBD=

180°-120°

2

=30°，
于是DP=tan30°•AD=

1

2

tan30°•AB，
即|

4ac-b2

4a

|=

1

2

×

3

3

×

b2-4ac

|a|

，
两边平方得，

(4ac-b2)2

16a2

=

b2-4ac

12a2

，
去分母得，3（b²-4ac）²=4（b²-4ac），
移项得，3（b²-4ac）²-4（b²-4ac）=0，
（b²-4ac）[3（b²-4ac）-4]=0，
解得b²-4ac=0或b²-4ac=

4

3

．
由于抛物线y=ax²+bx+c与x轴交于A，B两点，故△＞0，
即b²-4ac=

4

3

．
故答案为

4

3

．