题目内容
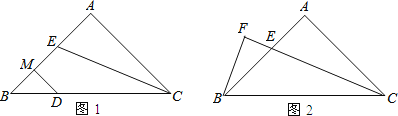
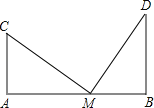
【题目】如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
【答案】这个人从B点到M点运动了3s.
【解析】
试题分析:根据∠CMD=90°,利用互余关系可以得出:∠ACM=∠DMB,证明三角形全等的另外两个条件容易看出.利用全等的性质可求得AC=BM=3,从而求得运动时间.
解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°
∴∠CMA+∠ACM=90°,
∴∠ACM=∠DMB,
在Rt△ACM和Rt△BMD中,
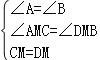 ,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴AC=BM=3m,
∴他到达点M时,运动时间为3÷1=3(s).
答:这个人从B点到M点运动了3s.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目