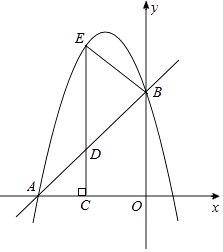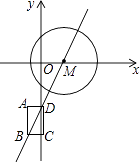��Ŀ����
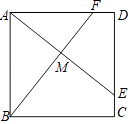
����Ŀ����1����ͼ1��AB��CD����MΪֱ��AB��CD��ȷ����ƽ���ڵ�һ�㣬����A105����M108����ֱ��д����C�Ķ��� ��
��2����ͼ2��AB��CD����PΪֱ��AB��CD��ȷ����ƽ���ڵ�һ�㣬��E��ֱ��CD�ϣ�ANƽ�֡�PAB������AN�ķ����ӳ��߽���PCE��ƽ������M������P30�����AMC�Ķ�����
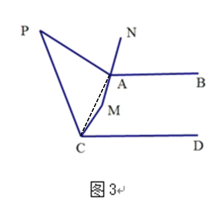
��3����ͼ3����P��ֱ��AB��CD��ͬһƽ���ڣ�ANƽ�֡�PAB������AN�ķ����ӳ��߽���PCD��ƽ������M����AMC180![]() P����֤��AB��CD��
P����֤��AB��CD��

���𰸡���1��![]() ����2��
����2��![]() ����3��֤�����̼�����
����3��֤�����̼�����
��������
��1��ֱ�����Ӹ�����AC����������ε��ڽǺ��Լ�ƽ���ߵ�ͬ���ڽǼ�����⣻
��2���ӳ�BA��CP����Q����CQ��AM���ڵ�H���ȸ���ANƽ�֡�PAB�����������ε���ǺͶԶ��ǣ��ú���BAN��ʽ������ʾ��MHC���١�AB��CD���õ�![]() ��ͨ��CMƽ�֡�PCE���õ���MCH�����ú���BAN��ʽ������ʾ��������������ε��ڽǺͼ�������𰸣�
��ͨ��CMƽ�֡�PCE���õ���MCH�����ú���BAN��ʽ������ʾ��������������ε��ڽǺͼ�������𰸣�
��3�����Ӹ�����AC����![]() ��
��![]()
![]()
![]() �������֪AMC180
�������֪AMC180![]() P���õ�
P���õ�![]() ��������
��������![]() ��ֵ��ͨ����ƽ���߾�֪����
��ֵ��ͨ����ƽ���߾�֪����![]() ��������
��������![]() ���͵õ���AB��CD��
���͵õ���AB��CD��
�⣺��1����ͼ������AC��
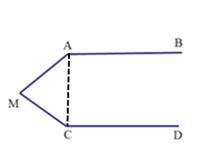
��![]() ��
��![]() ��
��
��AB��CD��
![]() ��
��
![]() ��
��
�ߡ�A105����M108��
��![]() ��
��
��2����ͼ���ӳ�BA��CP����Q����CQ��AM���ڵ�H��

��ANƽ�֡�PAB��
![]() ��
��
![]() ��
��
�ߡ�P30��
��![]() ��
��
![]() ��
��
��AB��CD��
![]() ��
��
��CMƽ�֡�PCE��
![]() ��
��
![]() ��
��![]() ��
��
��3����ͼ������AC��
��![]() ��
��![]() ��
��
��AMC180![]() P��
P��
![]() ��
��
![]() ��
��
��![]() ��
��
��ANƽ�֡�PAB��MCƽ�֡�PCD��
![]() ��
��
![]() ��
��
![]() ��
��
��AB��CD��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�