Question

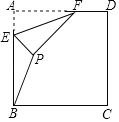
【题目】如图，四边形ABCD是边长为4的正方形，若AF＝3，E为AB上一个动点，把△AEF沿着EF折叠，得到△PEF，若△BPE为直角三角形，则BP的长度为_____．

Answer 1

【答案】2或．

【解析】

根据题意可得分两种情况讨论：①当∠BPE＝90°时，点B、P、F三点共线，②当∠PEB＝90°时，证明四边形AEPF是正方形，进而可求得BP的长．

根据E为AB上一个动点，

把△AEF沿着EF折叠，得到△PEF，

若△BPE为直角三角形，

分两种情况讨论：

①当∠BPE＝90°时，如图1，

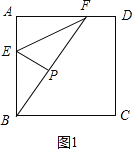
点B、P、F三点共线，

根据翻折可知：

∵AF＝PF＝3，AB＝4，

∴BF＝5，

∴BP＝BF﹣PF＝5﹣3＝2；

②当∠PEB＝90°时，如图2，

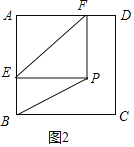
根据翻折可知：

∠FPE＝∠A＝90°，

∠AEP＝90°，

AF＝FP＝3，

∴四边形AEPF是正方形，

∴EP＝3，BE＝AB﹣AE＝4﹣3＝1，

∴BP＝＝＝．

综上所述：BP的长为：2或．

故答案为：2或．