题目内容
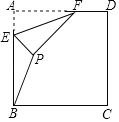
【题目】已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B、C重合),以AD为边做正方形ADEF,连接CF.
(1)如图①,当点D在线段BC上时,直接写出线段CF、BC、CD之间的数量关系 .
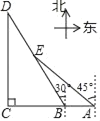
(2)如图②,当点D在线段BC的延长线上时,其他件不变,则(1)中的三条线段之间的数量关系还成立吗?如成立,请予以证明,如不成立,请说明理由;
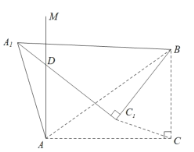
(3)如图③,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC两侧,其他条件不变;若正方形ADEF的边长为4,对角线AE、DF相交于点O,连接OC,请直接写出OC的长度.

【答案】(1)CF+CD=BC;(2)CF+CD=BC不成立,存在CF﹣CD=BC,证明详见解析;(3)![]() .
.
【解析】
(1)△ABC是等腰直角三角形,利用SAS即可证明△BAD≌△CAF,从而证得CF=BD,据此即可证得;
(2)同(1)相同,利用SAS即可证得△BAD≌△CAF,从而证得BD=CF,即可得到CF﹣CD=BC;
(3)先证明△BAD≌△CAF,进而得出△FCD是直角三角形,然后根据正方形的性质即可求得DF的长,再根据直角三角形斜边上中线的性质即可得到OC的长.
(1)∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,
 ,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∵BD+CD=BC,
∴CF+CD=BC;
故答案为:CF+CD=BC;
(2)CF+CD=BC不成立,存在CF﹣CD=BC;
理由:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,
 ,
,
∴△BAD≌△CAF(SAS)
∴BD=CF
∴BC+CD=CF,
∴CF﹣CD=BC;
(3)∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠BAF,∠CAF=90°﹣∠BAF,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,
 ,
,
∴△BAD≌△CAF(SAS),
∴∠ACF=∠ABD,
∵∠ABC=45°,
∴∠ABD=135°,
∴∠ACF=∠ABD=135°,
∴∠FCD=135°﹣45°=90°,
∴△FCD是直角三角形.
∵正方形ADEF的边长4且对角线AE、DF相交于点O.
∴DF=![]() AD=4
AD=4![]() ,O为DF中点.
,O为DF中点.
∴Rt△CDF中,OC=![]() DF=
DF=![]() ×
×![]() =
=![]() .
.

 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】如图,E为半圆O直径AB上一动点,AB=6,C为半圆上一定点,连接AC和BC,AD平分∠CAB交BC于点D,连接CE和DE.小红根据学习函数经验,分别对线段AE,CE,DE的长度之间的关系进行了探究.下面是小红的探究过程,请将它补充完整:
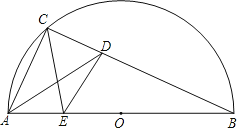
(1)对于点E在直径AB上的不同位置,画图,测量,得到了线段AE,CE,DE的长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
CE/cm | 2.50 | 2.28 | 2.50 | 3.00 | 3.72 | 4.64 | 5.44 |
DE/cm | 2.98 | 2.29 | 1.69 | 1.69 | 2.18 | 3.05 | 3.84 |
AE/cm | 0.00 | 0.87 | 2.11 | 3.02 | 4.00 | 5.12 | 6.00 |
在AECE,DE的长度这三个量中,确定 长度是自变量,自变量的取值范围是 ;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定函数的图象;
(3)结合函数的图象,解决问题:当△ACE为等腰三角形时,AE的长度约为 cm(结果精确到0.01).