题目内容
【题目】如图:O是直线AB上一点,∠AOC=50°,OD是∠BOC的角平分线,OE⊥OC于点O.求∠DOE的度数.(请补全下面的解题过程)
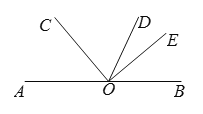
解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= °.
∵ OD是∠BOC的角平分线,
∴∠COD= ∠BOC .( )
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= °.( )
∴∠DOE=∠COE-∠COD= ° .
【答案】130,![]() ,角平分线的定义,90,垂直的定义,25
,角平分线的定义,90,垂直的定义,25
【解析】
先求出∠BOC的度数,再根据OD是∠BOC的角平分线得出∠COD的度数,然后根据OE⊥OC,得出∠COE,最后根据∠DOE=∠COE-∠COD得出答案.
解:解:∵O是直线AB上一点,∠AOC=50°,
∴∠BOC=180°-∠AOC= 130 °.
∵ OD是∠BOC的角平分线,
∴∠COD= ![]() ∠BOC .( 角平分线的定义)
∠BOC .( 角平分线的定义)
∴∠COD=65°.
∵OE⊥OC于点O,(已知).
∴∠COE= 90 °.( 垂直的定义)
∴∠DOE=∠COE-∠COD= 25 ° .

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目