题目内容
【题目】综合与实践
问题背景
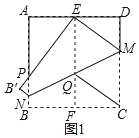
折纸是一种许多人熟悉的活动，将折纸的一边二等分、四等分都是比较容易做到的，但将一边三等分就不是那么容易了，近些年，经过人们的不懈努力，已经找到了多种将正方形折纸一边三等分的精确折法，最著名的是由日本学者芳贺和夫发现的三种折法，现在被数学界称之为芳贺折纸三定理．其中，芳贺折纸第一定理的操作过程及内容如下（如图1）：
操作1：將正方形ABCD对折，使点A与点D重合，点B与点C重合．再将正方形ABCD展开，得到折痕EF；
操作2：再将正方形纸片的右下角向上翻折，使点C与点E重合，边BC翻折至B'E的位置，得到折痕MN，B'E与AB交于点P．则P即为AB的三等分点，即AP：PB=2：1．
解决问题
（1）在图1中，若EF与MN交于点Q，连接CQ．求证：四边形EQCM是菱形；
（2）请在图1中证明AP：PB=2：l．
发现感悟
若E为正方形纸片ABCD的边AD上的任意一点，重复“问题背景”中操作2的折纸过程，请你思考并解决如下问题：
（3）如图2．若
=2．则
= ；
（4）如图3，若=3，则= ；
（5）根据问题（2），（3），（4）给你的启示，你能发现一个更加一般化的结论吗？请把你的结论写出来，不要求证明．
【答案】(1)见解析；(2)见解析；(3)4;(4)6;(5)见解析.
【解析】分析：（1）由折叠可得，CM=EM，∠CMQ=∠EMQ，四边形CDEF是矩形，由CM=EQ，CM∥QE，可证四边形EQCM是平行四边形，进而证明四边形EQCM是菱形；
（2）设正方形ABCD的边长为1，CM=x，则EM=x，DM=1﹣x，在Rt△DEM中，由勾股定理可求得x的值，由△AEP∽△DME，列比例式求出AP的值，进而求出PB的值，从而结论可求；
（3）设正方形ABCD的边长为1，CM=x，则EM=x，DM=1﹣x，在Rt△DEM中，由勾股定理可得x的值，由△AEP∽△DME，可得AP的值和BP的值，进而求得结论.
（4）与（3）相同的方法求解即可；
（5）与（3）相同的方法求解即可；
详解：（1）由折叠可得，CM=EM，∠CMQ=∠EMQ，四边形CDEF是矩形，
∴CD∥EF，
∴∠CMQ=∠EQM，
∴∠EQM=∠EMQ，
∴ME=EQ，
∴CM=EQ，
又∵CM∥QE，
∴四边形EQCM是平行四边形，
又∵CM=EM，
∴四边形EQCM是菱形；
（2）如图1，设正方形ABCD的边长为1，CM=x，则EM=x，DM=1﹣x，
在Rt△DEM中，由勾股定理可得：EM2=ED2+DM2，
即x2=（
）2+（1﹣x）2，解得x=
，
∴CM=，DM=
，
∵∠PEM=∠D=90°，
∴∠AEP+∠DEM=90°，∠DEM+∠EMD=90°，
∴∠AEP=∠DME，
又∵∠A=∠D=90°，
∴△AEP∽△DME，
∴
=
，即
，解得AP=
，
∴PB=
，
∴AP：PB=2：l．
（3）如图2，设正方形ABCD的边长为1，CM=x，则EM=x，DM=1﹣x，
在Rt△DEM中，由勾股定理可得：EM2=ED2+DM2，
即x2=（）2+（1﹣x）2，解得x=
，
即CM=，
∴DM=
，
由△AEP∽△DME，可得
=
，即
，解得AP=
，
∴PB=
，
∴
=4，
故答案为：4；
（4）如图3，同理可得AP=
，PB=
，
∴=6，
故答案为：6；
（5）根据问题（2），（3），（4），可得当
（n为正整数），则
．
理由：设正方形ABCD的边长为1，CM=x，则EM=x，DM=1﹣x，
在Rt△DEM中，由勾股定理可得：EM2=ED2+DM2，
即x2=（
）2+（1﹣x）2，解得x=
，
∴DM=1﹣CM=
，
由△AEP∽△DME，可得
=，即
，解得AP=
，
∴PB=
，
∴
．
