Question

【题目】已知等腰三角形的周长是，底边是腰长的函数。

（1）写出这个函数的关系式；

（2）求出自变量的取值范围；

（3）当为等边三角形时，求的面积。

Answer 1

【答案】（1）y=18-2x，（2），（3）cm2.

【解析】

（1）根据等腰三角形周长公式可求出底边长与腰的函数关系式；

（2）由三角形两边之和大于第三边的关系可知x的取值范围；

（3）当为等边三角形时， AB=BC=AC=6，根据勾股定理求出三角形的高，然后根据三角形的面积公式求解即可.

（1）等腰三角形的底边长为y、腰长为x，

依题意和已知，有：

∵y+2x=18，

∴y=18-2x；

（2）∵，

∴18-2x>0，

∴x<9，

另：依据三角形的性质有：，

∴.

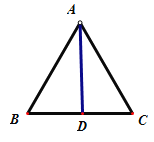
（3）当为等边三角形时， AB=BC=AC=6cm,

作AD⊥BC于点D，则∠BAD=30°，BD=3cm,

∴AD=cm，

∴ cm2.