题目内容
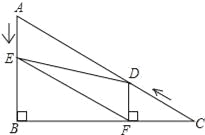
【题目】如图,在Rt△ABC中,∠B=90°,BC=![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.

【答案】见解析
【解析】试题分析: (1)在△DFC中,∠DFC=90°,∠C=30°,由已知条件求证;
(2)求得四边形AEFD为平行四边形,若使AEFD为菱形则需要满足的条件及求得;
(3)①∠EDF=90°时,四边形EBFD为矩形.在直角三角形AED中求得AD=2AE即求得.
②∠DEF=90°时,由(2)知EF∥AD,则得∠ADE=∠DEF=90°,求得AD=AEcos60°列式得.
③∠EFD=90°时,此种情况不存在.
(1)证明:在△DFC中,∠DFC=90°,∠C=30°,DC=2t,
∴DF=t.
又∵AE=t,
∴AE=DF.
(2)解:能.理由如下:
∵AB⊥BC,DF⊥BC,
∴AE∥DF.
又AE=DF,
∴四边形AEFD为平行四边形.
∵AB=BCtan30°=![]() =5,
=5,
∴AC=2AB=10.
∴AD=AC﹣DC=10﹣2t.
若使AEFD为菱形,则需AE=AD,
即t=10﹣2t,t=![]() .
.
即当t=![]() 时,四边形AEFD为菱形.
时,四边形AEFD为菱形.
(3)解:①∠EDF=90°时,四边形EBFD为矩形.
在Rt△AED中,∠ADE=∠C=30°,
∴AD=2AE.
即10﹣2t=2t,t=![]() .
.
②∠DEF=90°时,由(2)四边形AEFD为平行四边形知EF∥AD,
∴∠ADE=∠DEF=90°.
∵∠A=90°﹣∠C=60°,
∴AD=AEcos60°.
即10﹣2t=![]() t,t=4.
t,t=4.
③∠EFD=90°时,此种情况不存在.
综上所述,当t=![]() 秒或4秒时,△DEF为直角三角形.
秒或4秒时,△DEF为直角三角形.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案






