题目内容
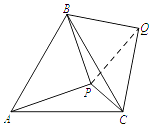
【题目】如图,P是等边△ABC内的一点,且PA=5,PB=4,PC=3,将△APB绕点B逆时针旋转,得到△CQB.求: 
(1)点P与点Q之间的距离;
(2)求∠BPC的度数.
【答案】
(1)解:连结PQ,如图,
∵△ABC是等边三角形
∴∠ABC=60°,BA=BC,
∵△QCB是△PAB绕点B逆时针旋转得到的,
∴BP=BQ,∠PBQ=∠ABC=60°,CQ=AP=5,
∵BP=BQ=4,∠PBQ=60°,
∴△PBQ是等边三角形,
∴PQ=PB=4
(2)解:∵QC=5,PC=3,PQ=4,
而32+42=52,
∴PC2+PQ2=CQ2,
∴△PCQ是直角三角形,且∠QPC=90°,
∵△PBQ是等边三角形,
∴∠BPQ=60°,
∴∠BPC=∠BPQ+∠QPC=60°+90°=150°.
【解析】(1)连结PQ,如图,根据等边三角形得性质得∠ABC=60°,BA=BC,再利用旋转的性质得BP=BQ,∠PBQ=∠ABC=60°,CQ=AP=5,BP=BQ=4,∠PBQ=60°,于是可判断△PBQ是等边三角形,所以PQ=PB=4;(2)先利用勾股定理的逆定理证明△PCQ是直角三角形,且∠QPC=90°,再加上∠BPQ=60°,然后计算∠BPQ+∠QPC即可.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握旋转的性质(①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了)的相关知识才是答题的关键.

练习册系列答案
相关题目






