题目内容
【题目】如图,已知 ![]() ABC,以AB为直径的圆O分别交AC于D,交BC于E,连接ED,若ED=EC.
ABC,以AB为直径的圆O分别交AC于D,交BC于E,连接ED,若ED=EC.
求证:AB=AC.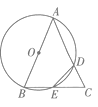
【答案】证明:∵ ![]() ,
,
∴ ![]()
∵四边形ABED内接于圆,
∴∠B+∠EDA=180°
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]()
【解析】根据等边对等角得出 ∠ E D C = ∠ C,根据圆的内接四边形的对角互补得出∠B+∠EDA=180°,根据邻补角的定义得出∠ E D C + ∠ E D A = 180 ° ,根据同角的补角相等得出 ∠ B = ∠ E D C ,从而得出 ∠ B = ∠ C ,根据等角对等边得出A B = A C。
【考点精析】通过灵活运用余角和补角的特征和圆内接四边形的性质,掌握互余、互补是指两个角的数量关系,与两个角的位置无关;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形即可以解答此题.

练习册系列答案
相关题目