题目内容
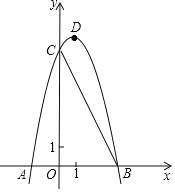
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0),与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.
(1)求抛物线的解析式;
(2)若PN:PM=1:4,求m的值;
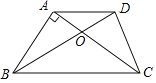
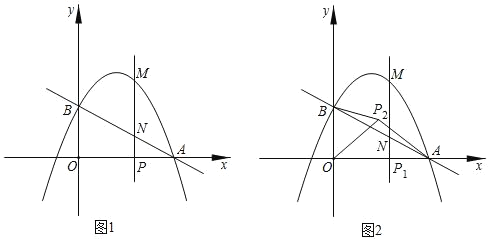
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)m=3;(3)
;(2)m=3;(3)![]()
【解析】
(1)本题需先根据图象过A点,代入即可求出解析式;(2)由△OAB∽△PAN可用m表示出PN,且可表示出PM,由条件可得到关于m的方程,则可求得m的值;(3)在y轴上取一点Q,使![]() ,可证的△P2OB∽△QOP2,则可求得Q点坐标,则可把AP2+
,可证的△P2OB∽△QOP2,则可求得Q点坐标,则可把AP2+![]() BP2转换为AP2+QP2,利用三角形三边关系可知当A、P2、Q三点在一条线上时,有最小值,则可求出答案.
BP2转换为AP2+QP2,利用三角形三边关系可知当A、P2、Q三点在一条线上时,有最小值,则可求出答案.
解:(1)∵A(4,0)在抛物线上,
∴0=16a+4(a+2)+2,解得a=﹣![]() ,
,
∴抛物线的解析式为y=![]() ;
;
(2)∵![]()
∴令x=0可得y=2,
∴OB=2,
∵OP=m,
∴AP=4﹣m,
∵PM⊥x轴,
∴△OAB∽△PAN,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵M在抛物线上,
∴PM=![]() +2,
+2,
∵PN:MN=1:3,
∴PN:PM=1:4,
∴![]() ,
,
解得m=3或m=4(舍去);
(3)在y轴上取一点Q,使![]() ,如图,
,如图,
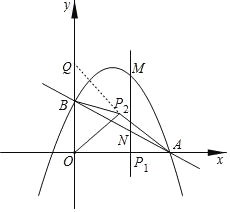
由(2)可知P1(3,0),且OB=2,
∴![]() ,且∠P2OB=∠QOP2,
,且∠P2OB=∠QOP2,
∴△P2OB∽△QOP2,
∴![]() ,
,
∴当Q(0,![]() )时,QP2=
)时,QP2=![]() ,
,
∴AP2+![]() BP2=AP2+QP2≥AQ,
BP2=AP2+QP2≥AQ,
∴当A、P2、Q三点在一条线上时,AP2+QP2有最小值,
∵A(4,0),Q(0,![]() ),
),
∴AQ=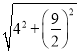 =
=![]() ,
,
即AP2+![]() BP2的最小值为
BP2的最小值为![]()

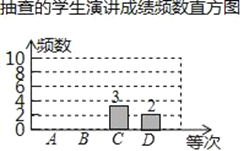
【题目】某校为庆祝“五四青年节”,在2018年4月底组织该校学生举办了“传承五四精神共建和谐社土会”的演讲比赛.为了解学生在演讲比赛中的成绩情况,学校随机抽取了部分学生的演讲比赛成绩进行统计(满分:100分,等次:A.优秀:90~100分;B.良好:80﹣89分;C.一般:60﹣79分;D.较差:60分以下,不含60分)得到如下不完整的图表:
等次 | 频数 | 频率 |
A | a | 0.25 |
B | b | 0.5 |
C | 3 | m |
D | 2 | 0.1 |
根据以上信息解答下列问题
(1)表中a=_____,b=_____,m=_______,并补全频数分布直方图;
(2)根据抽查学生演讲成绩频数统计表制作的扇形统计图中,表示C等次部分的扇形中心角的度数是_______;
(3)若A等次中有2名女生,其余为男生,学校准备从A等次学生中抽取2名学生组成演讲组合参加全市“五四青年杯”演讲比赛,求恰好抽取1名男生和1名女生的概率.