题目内容
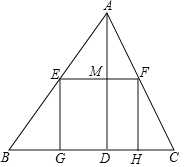
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的⊙O与AC相交于点D,过点D作DE⊥BC交AB延长线于点E,垂足为点F.
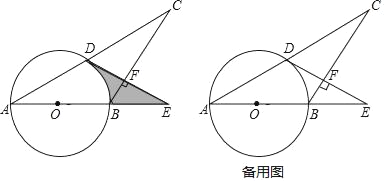
(1)证明:DE是⊙O的切线;
(2)若BE=4,∠E=30°,求由![]() 、线段BE和线段DE所围成图形(阴影部分)的面积,
、线段BE和线段DE所围成图形(阴影部分)的面积,
(3)若⊙O的半径r=5,sinA=![]() ,求线段EF的长.
,求线段EF的长.
【答案】(1)见解析 (2)8![]() (3)
(3)![]()
【解析】分析:(1)连接BD、OD,由AB=BC及∠ADB=90°知AD=CD,根据AO=OB知OD是△ABC的中位线,据此知OD∥BC,结合DE⊥BC即可得证;
(2)设⊙O的半径为x,则OB=OD=x,在Rt△ODE中由sinE=![]() 求得x的值,再根据S阴影=S△ODE-S扇形ODB计算可得答案.
求得x的值,再根据S阴影=S△ODE-S扇形ODB计算可得答案.
(3)先证Rt△DFB∽Rt△DCB得![]() ,据此求得BF的长,再证△EFB∽△EDO得
,据此求得BF的长,再证△EFB∽△EDO得![]() ,据此求得EB的长,继而由勾股定理可得答案.
,据此求得EB的长,继而由勾股定理可得答案.
详解:(1)如图,连接BD、OD,
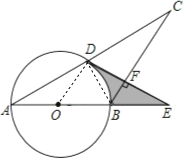
∵AB是⊙O的直径,
∴∠BDA=90°,
∵BA=BC,
∴AD=CD,
又∵AO=OB,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)设⊙O的半径为x,则OB=OD=x,
在Rt△ODE中,OE=4+x,∠E=30°,
∴![]() ,
,
解得:x=4,
∴DE=4![]() ,S△ODE=
,S△ODE=![]() ×4×4
×4×4![]() =8
=8![]() ,
,
S扇形ODB=![]() ,
,
则S阴影=S△ODE-S扇形ODB=8![]() -
-![]() ;
;
(3)在Rt△ABD中,BD=ABsinA=10×![]() =2
=2![]() ,
,
∵DE⊥BC,
∴Rt△DFB∽Rt△DCB,
∴![]() ,即
,即![]() ,
,
∴BF=2,
∵OD∥BC,
∴△EFB∽△EDO,
∴![]() ,即
,即![]() ,
,
∴EB=![]() ,
,
∴EF=![]() .
.

【题目】某公司招聘人才,对应聘者分别进行阅读能力、思维能力和表达能力三项测试,其中甲、乙两人的成绩如表(单位:分):
项目人员 | 阅读能力 | 思维能力 | 表达能力 |
甲 | 93 | 86 | 73 |
乙 | 95 | 81 | 79 |
(1)若根据三项测试的平均成绩在甲、乙两人中录用一人,那么谁将能被录用?
(2)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2的比确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(3)公司按照(2)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值,如最右边一组分数x为:85≤x<90),并决定由高分到低分录用8名员工,甲、乙两人能否被录用?请说明理由,并求出本次招聘人才的录用率.
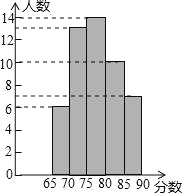
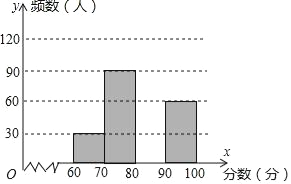
【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
组别 | 分数段(分) | 频数 | 频率 |
A组 | 60≤x<70 | 30 | 0.1 |
B组 | 70≤x<80 | 90 | n |
C组 | 80≤x<90 | m | 0.4 |
D组 | 90≤x<100 | 60 | 0.2 |
(1)在表中:m= ,n= ;
(2)补全频数分布直方图;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.