题目内容
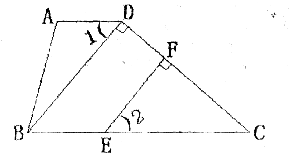
如图,Rt△AB′C′是由Rt△ABC绕点A顺时针旋转得到的,连结CC′交斜边于点E,CC′的延长线交BB′于点F。

(1)若AC=3,AB=4,求
(2)证明:△ACE∽△FBE;
(3)设∠ABC= ,∠CAC′=
,∠CAC′= ,试探索
,试探索 、
、 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。

(1)若AC=3,AB=4,求

(2)证明:△ACE∽△FBE;
(3)设∠ABC=
 ,∠CAC′=
,∠CAC′= ,试探索
,试探索 、
、 满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。
满足什么关系时,△ACE与△FBE是全等三角形,并说明理由。(1) (2)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
(2)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
∴△ACE∽△FBE(3)
 =
= 时△ACE≌△FBE。
时△ACE≌△FBE。
 (2)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
(2)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF∴△ACE∽△FBE(3)

 =
= 时△ACE≌△FBE。
时△ACE≌△FBE。试题分析:解(1)∵Rt△AB′C′是由Rt△ABC绕点A旋转得到的
∴AC=AC′,∠CAC′=∠BAB′,AB=AB′,∴

∴△CAC′∽△BAB′,∴

(2)由(1)可知△CAC′∽△BAB′,∴∠ACE=∠EBF,而∠AEC=∠BEF
∴△ACE∽△FBE
(3)当
 =2
=2 时,△ACE与△FBE全等
时,△ACE与△FBE全等由(1)可知△CAC′是等腰三角形,∠ACC′=

∴∠BCE=90°-∠ACC′=

 =
= ,∠ABC=
,∠ABC= ,∴∠BCE=∠ABC
,∴∠BCE=∠ABC∴BE=CE,又△ACE∽△FBE,∴△ACE≌△FBE
点评:本题难度中等,主要考查学生对相似三角形性质与全等三角形判定等知识点的掌握与运用能力,为中考常考题型,要注意数形结合应用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
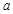 、b、c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③
、b、c,下列条件:①∠A=∠B-∠C;②∠A:∠B:∠C=3:4:5;③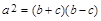 ;④
;④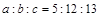 ,其中能判断△ABC是直角三角形的个数有( )
,其中能判断△ABC是直角三角形的个数有( )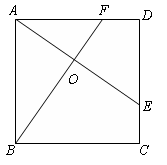
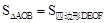 中正确的有
中正确的有