题目内容
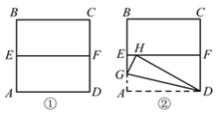
【题目】将一张边长为2的正方形纸片ABCD对折,设折痕为EF(如图①);再沿过点D的折痕将∠A翻折,使得点A落在EF上的点H处(如图②),折痕交AE于点G,则EG的长度是___________.
【答案】![]()
【解析】
由于正方形纸片ABCD的边长为2,所以将正方形ABCD对折后AE=DF=1,由翻折不变性的原则可知AD=DH=2,AG=GH,在Rt△DFH中利用勾股定理可求出HF的长,进而求出EH的长,再设EG=x,在Rt△EGH中,利用勾股定理即可求解.
∵正方形纸片ABCD的边长为2,
∴将正方形ABCD对折后AE=DF=1,
∵△GDH是△GDA沿直线DG翻折而成,
∴AD=DH=2,AG=GH,
在Rt△DFH中,
![]()
∴![]()
在Rt△EGH中,设EG=x,则GH=AG=1x,
∴![]()
即![]()
解得![]()
故答案为:![]()

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目