题目内容
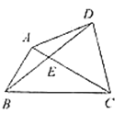
【题目】如图,已知 DE∥BC,CD 与 BE 相交于点 O,并且 S△DOE:S△COB=4:9,
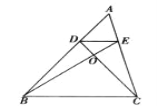
(1)求 AE:AC 的值;
(2)求△ADE 与四边形 DBCE 的面积比。
【答案】(1) AE:AC=2:3;(2)4:5.
【解析】
根据相似三角形面积比与边长比的关系解答此题.
(1)∵ED∥BC,
∴△DOE∽△COB,△AED∽△ACB.
∵△DOE∽△COB,S△DOE:S△COB=4:9,
∴ED:BC=2:3.
∵△AED∽△ACB,
∴ED:BC=AE:AC.
∵ED:BC=2:3,ED:BC=AE:AC,
∴AE:AC=2:3.
(2)∵△AED∽△ACB AE:AC=2:3
∴S△ADE:S△ACB=4:9
∴S△ADE:S 四 DBCE=4:5

练习册系列答案
相关题目