题目内容
【题目】如图,CN是等边△ABC的外角∠ACM内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(Ⅰ)依题意补全图形.
(Ⅱ)若∠ACN=α,求∠BDC的大小(用含α的式子表示).
(Ⅲ)若PA=x,PC=y,求PB的长度(用x,y的代数式表示).
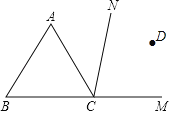
【答案】(Ⅰ)补图见解析;(Ⅱ)∠BDC=60°﹣α;(Ⅲ)PB= x+y.
【解析】
(Ⅰ)根据题意画图即可;
(Ⅱ)根据对称得:CN是AD的垂直平分线,则CA=CD,然后根据等腰三角形的性质和等边三角形的性质可得结论;
(Ⅲ)作辅助线,在PB上截取PF使PF=PC,连接CF,PA.先证明△CPF是等边三角形,再证明△BFC≌△APC,则BF=PA,由此即可解决问题.
解:(Ⅰ)如图,
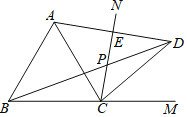
(Ⅱ) ∵点A与点D关于CN对称,
∴CN是AD的垂直平分线,
∴CA=CD,∠DCN=∠ACN=α,
∴∠ACD=2∠ACN=2α.
∵等边△ABC,
∴CA=CB,
∴CD=CB,
∴∠BDC=∠DBC.
∵∠ACB=60°.
∴∠BCD=∠ACB+∠ACD=60°+2α.
∴∠BDC=∠DBC=![]() (180°﹣∠BCD)=60°﹣α.
(180°﹣∠BCD)=60°﹣α.
(Ⅲ)在PB上截取PF使PF=PC,连接CF,PA
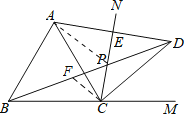
设∠ACN=α,
∵CA=CD,∠ACD=2α,
∴∠CDA=∠CAD=90°﹣α.
∵∠BDC=60°﹣α,
∴∠PDE=∠CDA﹣∠BDC=30°,
∵∠CPF=∠DPE=90°﹣∠PDE=60°.
∴△CPF是等边三角形.
∴CF=CP,∠PCF=60°,
∵∠PCF=∠ACB,
∴∠BCF=∠ACP,
∵CB=CA,CF=CP,
∴△BFC≌△APC(SAS),
∴BF=PA,
∴PB=PF+BF=PA+PC=x+y.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目