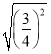题目内容
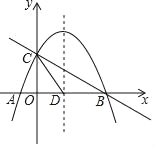
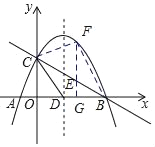
【题目】如图,抛物线y=﹣![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为_____.
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2),点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当四边形CDBF的面积最大时,E点的坐标为_____.
【答案】(2,1)
【解析】
由于四边形CDBF的面积等于△CDB的面积与△BCF的面积之和,当四边形CDBF的面积最大时,即△BCF最大,设点E的坐标为(x,y),利用点E的坐标表示出△BCF的面积即可求出点E的坐标.
过点E作EG⊥x轴于点G,交抛物线于F,
将A(﹣1,0),C(0,2)代入y=﹣![]() x2+mx+n
x2+mx+n
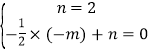
解得:
∴抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2
x+2
令y=0代入y=﹣![]() x2+
x2+![]() x+2,
x+2,
∴0=﹣![]() x2+
x2+![]() x+2
x+2
解得:x=﹣1或x=4
∴B(4,0)
∴OB=4
设直线BC的解析式为y=kx+b,
把B(4,0)和C(0,2)代入y=kx+b
∴![]()
解得: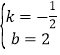
∴直线BC的解析式为:y=﹣![]() x+2,
x+2,
设E的坐标为:(x,﹣![]() x+2)
x+2)
∴F(x,﹣![]() x2+
x2+![]() x+2)
x+2)
∴EF=﹣![]() x2+
x2+![]() x+2﹣(﹣
x+2﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x2+2x,
x2+2x,
∴△BCF的面积为:![]() EFOB=2(﹣
EFOB=2(﹣![]() x2+2x)=﹣x2+4x=﹣(x﹣2)2+4
x2+2x)=﹣x2+4x=﹣(x﹣2)2+4
四边形CDBF的面积最大时,只需要△BCF的面积最大即可,
∴当x=2时,
△BCF的面积可取得最大值,
此时E的坐标为(2,1)
故答案是:(2,1).

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目