题目内容
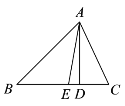
【题目】如图,在 Rt△ABC 中,∠ACB=90°,BC=5,点 P 在边 AB 上,连接 CP.将△BCP 沿直线CP 翻折后,点 B 恰好落在边 AC 的中点处,则点 P 到 AC 的距离是( )

A. 2.5 B. ![]() C. 3.5 D.
C. 3.5 D. ![]()
【答案】B
【解析】
作PN⊥AC,PM⊥BC,垂足分别为N、M, 点D为AC的中点, 根据折叠的性质得AD=AB=5, ∠BCP=∠ACP, 则AC=2AD=10, 根据角平分线定理得PM=PN, 然后利用三角形面积相等可求得PN的长.
解:如图, 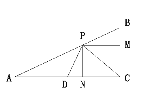
![]() 将△BCP 沿直线CP 翻折后,点 B 恰好落在边 AC 的中点处,假设这个点是D,
将△BCP 沿直线CP 翻折后,点 B 恰好落在边 AC 的中点处,假设这个点是D,
![]() 可得BC=CD=5,AC=2CD=10,
可得BC=CD=5,AC=2CD=10,
作PN⊥AC,PM⊥BC,垂足分别为N、M.则∠BCP=∠ACP ,PM=PN,
又Rt △ABC 中,∠BAC=90![]() ,BC=5,
,BC=5,
![]() BC=CD=5,AC=2CD=10,
BC=CD=5,AC=2CD=10,
![]() =
=![]() +
+![]() =
=![]()
![]() 5
5![]() 10=
10=![]()
![]() 5
5![]() PM+
PM+![]()
![]() 10
10![]() PN,
PN,
解得PN=![]() ,所以点M到AC的距离是
,所以点M到AC的距离是![]() .
.
故选:B.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目