题目内容
【题目】如图,正方形ABCD和正方形OPEF中,边AD与边OP重合,![]() ,
,![]() ,点M、N分别在正方形ABCD的边BC、CD上,且
,点M、N分别在正方形ABCD的边BC、CD上,且![]() .将正方形OPEF以每秒2个单位的速度向右平移,当点F与点B重合时,停止平移.设平移时间为t秒.
.将正方形OPEF以每秒2个单位的速度向右平移,当点F与点B重合时,停止平移.设平移时间为t秒.
(1)请求出t的取值范围;
(2)猜想:正方形OPEF的平移过程中,OE与NM的位置关系.并说明理由.
(3)连结DE、BE.当![]() 的面积等于7时,试求出正方形OPEF的平移时间t的值.
的面积等于7时,试求出正方形OPEF的平移时间t的值.


备用图
【答案】(1)![]() ;(2)OE⊥MN,证明见详解;(3)t的值为:
;(2)OE⊥MN,证明见详解;(3)t的值为:![]() 或
或![]() .
.
【解析】
(1)根据题意,当AD与OP重合时,可求出AF=OF=2,BF=6,然后求出时间的最大值,即可得到t的取值范围;
(2)连接AC,BD,OE,在运动过程中有OE∥AC,由∠CNM=45°=∠CDB,得到BD∥MN,由AC⊥BD,得到AC⊥MN,即可得到OE⊥MN;
(3)由勾股定理求出BD=![]() ,由面积公式,求出△BDE的高为
,由面积公式,求出△BDE的高为![]() ,连接DE,BE,连接OE与BD相交于点H,根据正方形OPEF求出OE的长度,然后得到OH的长度,由等腰三角形△OBH中,根据勾股定理求得OB的长度,然而OB=(8-2t),最后求出t的值.
,连接DE,BE,连接OE与BD相交于点H,根据正方形OPEF求出OE的长度,然后得到OH的长度,由等腰三角形△OBH中,根据勾股定理求得OB的长度,然而OB=(8-2t),最后求出t的值.
(1)根据题意,当AD与OP重合时,
∴![]() ,
,
∴![]() ,
,
当点F到达点B时的时间为:![]() (秒),
(秒),
∴![]() 的取值范围是:
的取值范围是:![]() ;
;
(2)OE与MN是垂直的关系;
如图,连接AC,BD,OE,
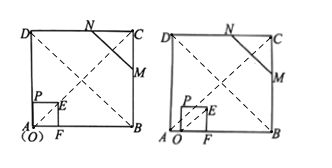
由平移性质得:OE∥AC,
由正方形性质可知,
∵∠CDB=45°=∠CNM
∴MN∥BD,
∵AC⊥BD,
∴AC⊥MN
∴OE⊥MN;
(3)连接DE,BE,连接OE与BD相交于点H,在正方形ABCD中,有AB=AD=8,
∴BD=![]() ,
,
由(2)知,OE⊥BD,则EH是△BDE的高,
由三角形面积公式,得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
① 当点E在BD的下方时,如下图:
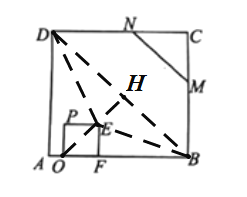
在正方形OPEF中,![]() ,
,
∴![]() ,
,
∵△OBH是等腰直角三角形,OH=BH
∵运动过程中,AO=2t,则OB=(8-2t)
由勾股定理得:![]() ,
,
∴![]() ,
,
解得:![]() ;
;
②当点E在BD的上方时,如图:
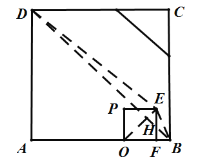
此时,![]() ,
,
由勾股定理得:![]() ,
,
解得:![]() ,
,
∴t的值为![]() 或
或![]() .
.

【题目】“端午节”期间,某商场购进A、B两种品牌的粽子共320袋,其中A品牌比B品牌多80袋.此两种粽子每袋的进价和售价如下表所示,已知销售八袋A品牌的粽子获利136元.(注;利润=售价-进价)
品牌 | A | B |
进价(元/袋) | m | 38 |
售价(元/袋) | 66 | 50 |
(1)试求出m的值.
(2)该商场购进A、B两种品牌的粽子各多少袋?
(3)该商场调整销售策略,A品牌的粽子每袋按原售价销售,B品牌的粽子每袋打折出售.如果购进的A、B两种品牌的粽子全部售出的利润不少于4360元,问B种品牌的粽子每袋最低打几折出售?