Question

【题目】已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①b2＞4ac；②abc＞0；③2a﹣b=0；④8a+c＜0；⑤9a+3b+c＜0，其中结论正确的是　 　．（填正确结论的序号）

Answer 1

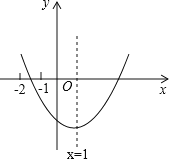
【答案】①②⑤

【解析】

试题①由图知：抛物线与x轴有两个不同的交点，则△=b2﹣4ac＞0，∴b2＞4ac。故①正确。

②抛物线开口向上，得：a＞0；

抛物线的对称轴为，b=﹣2a，故b＜0；

抛物线交y轴于负半轴，得：c＜0；

所以abc＞0。故②正确。

③∵抛物线的对称轴为，b=﹣2a，∴2a+b=0，故2a﹣b=0。故③错误。

④根据②可将抛物线的解析式化为：y=ax2﹣2ax+c（a≠0）；

由函数的图象知：当x=﹣2时，y＞0；即4a﹣（﹣4a）+c=8a+c＞0，故④错误。

⑤根据抛物线的对称轴方程可知：（﹣1，0）关于对称轴的对称点是（3，0）；

当x=﹣1时，y＜0，所以当x=3时，也有y＜0，即9a+3b+c＜0。故⑤正确。

综上所述，结论正确的有①②⑤。