题目内容
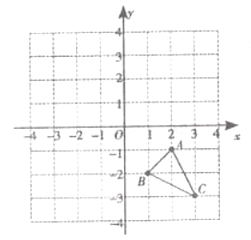
【题目】等边△ABC的边BC在射线BD上,动点P在等边△ABC的BC边上(点P与BC不重合),连接AP.
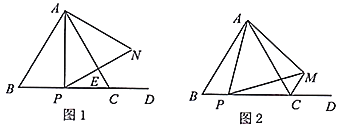
(1)如图1,当点P是BC的中点时,过点P作![]() 于E,并延长PE至N点,使得
于E,并延长PE至N点,使得![]() .①若
.①若![]() ,试求出AP的长度;
,试求出AP的长度;
②连接CN,求证![]() .
.
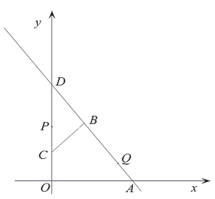
(2)如图2,若点M是△ABC的外角![]() 的角平分线上的一点,且
的角平分线上的一点,且![]() ,求证:
,求证:![]() .
.
【答案】(1)①AP![]() ;②证明见解析;(2)证明见解析.
;②证明见解析;(2)证明见解析.
【解析】
(1)①根据点P是BC的中点,利用等腰三角形三线合一的性质得AP⊥BC,再利用勾股定理即可求得答案;
②根据轴对称的性质,证得∠NCE=∠PCE=![]() ,从而证得结论;
,从而证得结论;
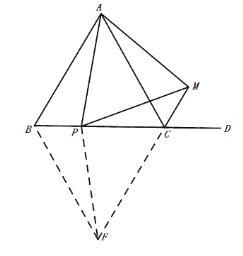
(2)作∠CBF=60°,BF与MC的延长线相交于点F,连接PF,证明△BFC是等边三角形,证得△ABP![]() △FBP,PM=PF,∠PMC=∠PFC,根据三角形外角的性质可得结论.
△FBP,PM=PF,∠PMC=∠PFC,根据三角形外角的性质可得结论.
(1)①在等边△ABC中,
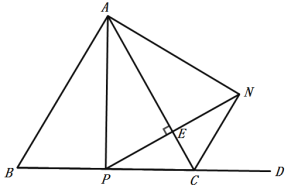
∵点P是BC的中点,![]() ,
,
∴AP⊥BC,![]() ,
,
∴AP=![]() ;
;
②∵![]() 且
且![]() ,
,
∴点N与点P关于直线AC对称,
∴∠NCE=∠PCE=![]() ,
,
∴∠NCD=180![]() ∠NCE
∠NCE![]() ∠PCE=
∠PCE=![]() ,
,
∴∠NCD=∠B=![]() ,
,
∴![]() ;
;
(2)作∠CBF=60°,BF与MC的延长线相交于点F,连接PF,如图:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60![]() ,
,
∴∠ACD=120![]() ,
,
∵CM平分∠ACD,
∴∠DCM=∠BCF=60![]() ,
,
∵∠CBF=60![]() ,
,
∴∠FBC=∠BCF=∠BFC=60![]() ,
,
∴△BFC是等边三角形,
∵△ABC和△BFC都是等边三角形,
∴AB=BC=BF,
在△ABP和△FBP中,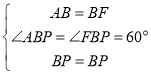 ,
,
∴△ABP![]() △FBP,
△FBP,
∴AP=PF,∠BAP=∠BFP,
∵AP=PM,
∴PM=PF,
∴∠PMC=∠PFC,
∵∠MCD=∠PMC +∠CPM=60![]() ,
,
∠BFC=∠BFP+∠PFC=60![]() ,
,
∴∠CPM=∠BFP =∠BAP,
∵∠APC=∠ABC+∠BAP=∠APM+∠CPM,
∴∠APM=60![]() .
.