题目内容
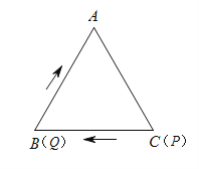
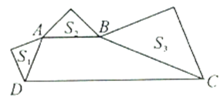
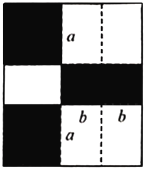
【题目】如图是两个全等的三角形纸片，其三边长之比为
，按图中方法分别将其对折，使折痕(图中虚线)过其中的一个顶点，且使该项点所在两边重合，记折叠后不重叠部分面积分别为
，已知
，则纸片的面积是（ ）
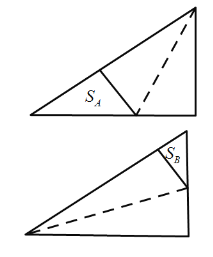
A.
B.
C.
D.
【答案】A
【解析】
设AC=FH=3x，则BC=GH=4x，AB=GF=5x，根据勾股定理即可求得CD的长，利用x表示出SA，同理表示出SB，根据
，即可求得x的值，进而求得三角形的面积．
解：如图，
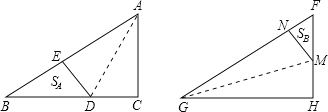
设AC=FH=3x，则BC=GH=4x，AB=GF=5x．
设CD=y，则BD=4x-y，DE=CD=y，
在直角△BDE中，BE=5x-3x=2x，
根据勾股定理可得：4x2+y2=（4x-y）2，
解得：y=
x，
则SA=
BEDE=×2xx=x2，
同理可得：SB=
x2，
∵SA-SB=10，
∴x2-x2=10，
∴x2=12，
∴纸片的面积是：×3x4x=6 x2=72．
故选A.
练习册系列答案
相关题目
