Question

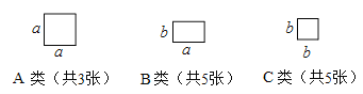
【题目】现有3张边长为的正方形纸片（类），5张边长为的矩形纸片（类），5张边长为的正方形纸片（类）．

我们知道：多项式乘法的结果可以利用图形的面积表示．

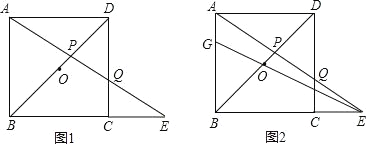
例如：就能用图①或图②的面积表示．

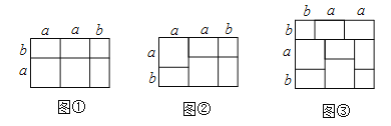
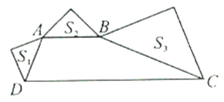
（1）请你写出图③所表示的一个等式：_______________；

（2）如果要拼一个长为，宽为的长方形，则需要类纸片_____张，需要类纸片_____张，需要类纸片_____张；

（3）从这13张纸片中取出若干张，每类纸片至少取出一张，把取出的这些纸片拼成一个正方形（按原纸张进行无缝隙，无重叠拼接），则拼成的正方形的边长最长可以是_______（用含的式子表示）．

Answer 1

【答案】（1）；（2）1，4，3；（3）

【解析】

（1）从整体和部分两方面表示该长方形的面积即可；

（2）根据拼成前后长方形的面积不变可先算出该长方形的面积再确定A类B类C类纸片的张数；

（3）由A类B类C类纸片的张数及面积可知构成的正方形的面积最大为，利用完全平方公式可得边长.

解：（1）从整体表示该图形面积为，从部分表示该图形面积为，所以可得；

（2）该长方形的面积为，A类纸片的面积为，B类纸片的面积为，C类纸片的面积为，所以需要类纸片1张，需要类纸片4张，需要类纸片3张；

（3）A类纸片的面积为，有3张；B类纸片的面积为，有5张；C类纸片的面积为，有5张，所以能构成的正方形的面积最大为，因为，所以拼成的正方形的边长最长可以是.