题目内容
【题目】填写下列解题过程中的推理根据:
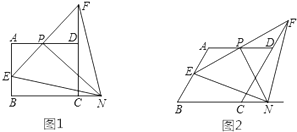
已知:如图,点F、E分别在AB、CD上,AE、DF分别与BC相交于H、G,∠A=∠D,∠1+∠2=180°.说明:AB∥CD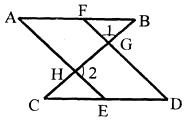
解:∵∠1=∠CGD()
∠1+∠2=180°
∴.
∴AE//FD ()
∴(两直线平行,同位角相等)
又∠A=∠D
∴∠D=∠BFD
∴()
【答案】对顶角相等;∠CGD+∠2=180°;同旁内角互补,两直线平行;∠A=∠BFD;AB//CD;内错角相等,两直线平行
【解析】根据对顶角,与平行线的性质与判定填空.
【考点精析】解答此题的关键在于理解对顶角和邻补角的相关知识,掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个,以及对平行线的判定的理解,了解同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
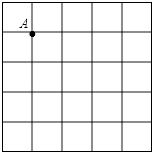
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图一:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |

(1)请将表一和图一中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.