题目内容
【题目】如图（1），在矩形ABCD中，AB=4，BC=6，P是AD的中点，N是BC延长线上一点，连结PN，过点P作PN的垂线，交AB于点E，交CD的延长线于点F，连结EN，FN，设CN=x，AE=y．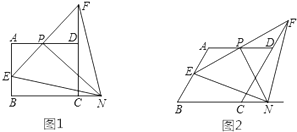
（1）求证：PE=PF；
（2）当0＜x＜ 
时，求y关于x的函数表达式；
（3）若将“矩形ABCD”变为“菱形ABCD”，如图（2），AB=BC=4，∠B=60°，当0＜x＜3时，其它条件不变，求此时y关于x的函数表达式．
【答案】
（1）
证明：∵P是AD的中点，四边形ABCD是矩形，
∴AP=DP，∠A=∠PDF=90°，
在△APE和△DPF中，
∵ 
，
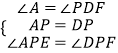∴△APE≌△DPF（ASA），
∴PE=PF
（2）
解：如图1，过点N作NQ⊥AD交AD延长线于Q，
∴四边形CDQN是矩形，
∴CN=DQ=x，CD=NQ=4，
又∵AD=BC=6，P是AD中点，
∴AP=PD=3，
∴PQ=3+x，
∵NP⊥EF，
∴∠APE+∠NPQ=90°，
∵∠APE+∠AEP=90°，
∴∠NPQ=∠PEA，
∵∠A=∠PQN=90°，
∴△APE∽△QNP，
∴ 
，即 
，
∴y= 
x+ 
（3）
解：如图2，过点N作NQ∥CD交AD延长线于点Q，
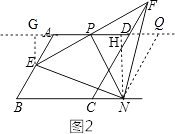
∴四边形CDQN是平行四边形，
∴CN=DQ=x，CD=NQ=4，
∵PD=PA= 
AD=2，
∴PQ=2+x，
过点N作NH⊥PQ于H，
∵∠DQN=∠DCN=∠B=60°，
∴HQ=NQcos∠DQN=4× =2，NH=NQsin∠DQN=4× 
=2 
，
∴PH=PQ﹣HQ=x，
过点E作EG⊥DA交DA延长线于G，
∵AE=y，∠GAE=∠B=60°，
∴AG=AEcos∠GAE= y，EG=AEsin∠GAE= y，
∴PG=PA+AG=2+ y，
∵∠EGP=∠PHN=∠EPN=90°，
∴∠EPG+∠PEG=∠EPG+∠NPD=90°，
∴∠PEG=∠NPD，
∴△PEG∽△NPD，
∴ 
，即 
，
∴y= 
【解析】（1）证△APE≌△DPF即可得；（2）过点N作NQ⊥AD交AD延长线于Q，可得四边形CDQN是矩形，从而表示出PQ、NQ的长，再证△APE∽△QNP可得 ，据此可得函数解析式；（3）过点N作NQ∥CD交AD延长线于点Q，可得四边形CDQN是平行四边形，据此知PQ=2+x、NQ=4，再过点N作NH⊥PQ于H，由∠DQN=60°得HQ=2、NH=2 ，从而表示出PH的长，过点E作EG⊥DA交DA延长线于G，由AE=y、∠GAE=∠B=60°得AG、EG的长，继而可得PG的长，最后证△PEG∽△NPD得 ，据此即可得答案．
