题目内容
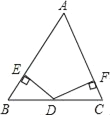
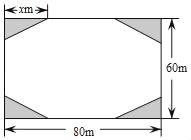
【题目】结合西昌市创建文明城市要求，某小区业主委员会决定把一块长80m，宽60m的矩形空地建成花园小广场，设计方案如图所示，阴影区域为绿化区（四块绿化区为全等的直角三角形），空白区域为活动区，且四周出口宽度一样，其宽度不小于36m，不大于44m，预计活动区造价60元/m2，绿化区造价50元/m2，设绿化区域较长直角边为xm．
（1）用含x的代数式表示出口的宽度；
（2）求工程总造价y与x的函数关系式，并直接写出x的取值范围；
（3）如果业主委员会投资28.4万元，能否完成全部工程？若能，请写出x为整数的所有工程方案；若不能，请说明理由．
（4）业主委员会决定在（3）设计的方案中，按最省钱的一种方案，先对四个绿化区域进行绿化，在实际施工中，每天比原计划多绿化11m2，结果提前4天完成四个区域的绿化任务，问原计划每天绿化多少m2．
【答案】（1）（80﹣2x）cm；（2）y＝＝﹣20x2+200x+288000，18≤x≤22；（3）能，所有方案如下：①较长直角边为20m，短直角边为10m，出口宽度为40m；②较长直角边为21m，短直角边为11m，出口宽度为38m；③较长直角边为22m，短直角边为12m，出口宽度为36m；（4）33m2
【解析】
（1）根据图形可得结论；（2）根据面积×造价可得绿化区和活动区的费用，相加可得y与x的关系式，根据所有长度都是非负数列不等式组可得x的取值范围；（3）业主委员会投资28.4万元，列不等式，结合二次函数的增减性可得结论；（4）先计算设计的方案中，最省钱的一种方案为x＝22时，计算绿化面积，根据题意列分式方程可得结论，注意方程要检验．
解：（1）由题意可得，
出口的宽度为；
（2）由题意可得，BC＝EF＝80﹣2x，
∴AB＝CD＝
＝x﹣10，
y＝50×4×
x（x﹣10）+60×[60×80﹣4×x（x﹣10）]＝﹣20x2+200x+288000，
∵36≤80﹣2x≤44，
∴18≤x≤22，
（3）﹣20x2+200x+288000≤284000，
x2﹣10x﹣200≥0，
设y＝x2﹣10x﹣200＝（x﹣5）2﹣225，
当y＝0时，x2﹣10x﹣200＝0，x＝20或﹣10，
∴当y≥0时，x≤﹣10或x≥20
由（2）知：18≤x≤22，
∴20≤x≤22，
所以业主委员会投资28.4万元，能完成全部工程，
所有工程方案如下：①较长直角边为20m，短直角边为10m，出口宽度为40m；
②较长直角边为21m，短直角边为11m，出口宽度为38m；
③较长直角边为22m，短直角边为12m，出口宽度为36m；
（4）y＝﹣20x2+200x+288000＝﹣20（x﹣5）2+288450，
在20≤x≤22中y随x的增大而减小，
∴当x＝22时，y有最小值，
绿化面积＝4××22×（22﹣10）＝528，
设原计划每天绿化xm2，则在实际施工中，每天绿化（x+11）m2，
则
＝4，
解得：x＝33或﹣44（舍），
经检验x＝33是原方程的解，
答：原计划每天绿化33m2．
阅读快车系列答案
