题目内容
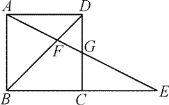
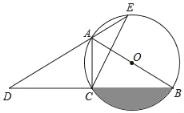
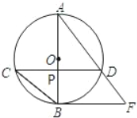
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点P,直线BF与AD的延长线交于点F,且∠AFB=∠ABC.
(1)求证:直线BF是⊙O的切线.
(2)若CD=2![]() ,OP=1,求线段BF的长.
,OP=1,求线段BF的长.
【答案】(1)证明见解析;(2)BF=![]() .
.
【解析】
(1)欲证明直线BF是⊙O的切线,只要证明AB⊥BF即可.
(2)连接OD,在Rt△ODE中,利用勾股定理求出由△APD∽△ABF,![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
(1)∵∠AFB=∠ABC,∠ABC=∠ADC,∴∠AFB=∠ADC,
∴CD∥BF,∴∠AFD=∠ABF,
∵CD⊥AB,∴AB⊥BF,∴直线BF是⊙O的切线.
(2)连接OD,∵CD⊥AB,∴PD=0.5CD=![]() ,
,
∵OP=1,∴OD=2,∵∠PAD=∠BAF,∠APO=∠ABF,∴△APD∽△ABF,
∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴BF=
,∴BF=![]() .
.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目