题目内容
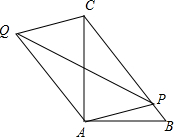 如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为
如图Rt△ABC中,∠BAC=90°,AB=3,AC=4,点P为BC上任意一点,连接PA,以PA,PC为邻边作平行四边形PAQC,连接PQ,则PQ的最小值为考点:相似三角形的判定与性质,垂线段最短,勾股定理,平行四边形的性质
专题:压轴题
分析:以PA,PC为邻边作平行四边形PAQC,由平行四边形的性质可知O是AC中点,PQ最短也就是PO最短,所以应该过O作BC的垂线P′O,然后根据△P′OC和△ABC相似,利用相似三角形的性质即可求出PQ的最小值.
解答:解: ∵∠BAC=90°,AB=3,AC=4,
∵∠BAC=90°,AB=3,AC=4,
∴BC=
=5,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴
=
,
∴
=
,
∴OP′=
,
∴则PQ的最小值为2OP′=
,
故答案为:
.
 ∵∠BAC=90°,AB=3,AC=4,
∵∠BAC=90°,AB=3,AC=4,∴BC=
| AC2+AB2 |
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴
| CO |
| BC |
| OP′ |
| AB |
∴
| 2 |
| 5 |
| OP′ |
| 3 |
∴OP′=
| 6 |
| 5 |
∴则PQ的最小值为2OP′=
| 12 |
| 5 |
故答案为:
| 12 |
| 5 |
点评:本题考查了勾股定理的运用、平行四边形的性质、相似三角形的判定和性质以及垂线段最短的性质,解题的关键是做高线各种相似三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知AB、CD是⊙O的直径,则四边形ACBD是( )
| A、正方形 | B、矩形 |
| C、菱形 | D、等腰梯形 |
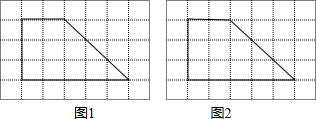
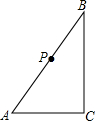
 在正方形网络图上(如图)有四个三角形,其中与△ABC相似(不包△ABC本身)的有( )
在正方形网络图上(如图)有四个三角形,其中与△ABC相似(不包△ABC本身)的有( )| A、0个 | B、1个 | C、2个 | D、3个 |

 如图,P是Rt△ABC斜边AB上的动点(P异于A、B),∠C=90°,∠B=30°,过点P的直线截△ABC,使截得的三角形与△ABC相似,当
如图,P是Rt△ABC斜边AB上的动点(P异于A、B),∠C=90°,∠B=30°,过点P的直线截△ABC,使截得的三角形与△ABC相似,当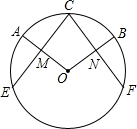 如图,在⊙O中,点C是弧AB的中点,过点C分别作半径OA、OB的垂线,交⊙O于E、F两点,垂足分别为M、N,求证:ME=NF.
如图,在⊙O中,点C是弧AB的中点,过点C分别作半径OA、OB的垂线,交⊙O于E、F两点,垂足分别为M、N,求证:ME=NF.