题目内容
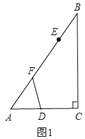
【题目】如图,四边形![]() 为菱形,点
为菱形,点![]() 为对角线
为对角线![]() 上的一个动点,连接
上的一个动点,连接![]() 并延长交射线
并延长交射线![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 是否存在这样一个菱形,当
是否存在这样一个菱形,当![]() 时,刚好
时,刚好![]() ?若存在,求出
?若存在,求出![]() 的度数;若不存在,请说明理由;
的度数;若不存在,请说明理由;
![]() 若
若![]() ,且当
,且当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的度数.
的度数.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
试题首先证明△DCE≌△BCE得∠EDC=∠EBC,根据DC∥AB得∠EDC=∠AFD,从而说明结论;根据DE=EC得出∠EDC=∠ECD,设∠EDC=∠ECD=∠CBE= x°,则∠CBF=2x°,根据BE⊥AF得出x的值,然后计算;当F在AB延长线上时,∠EFB为钝角,只能是BE=BF,通过三角形内角和求出未知数的值;当F在线段AB上时,∠EFB为钝角只能是FE=FB,然后进行计算.
试题解析:(1)∵△DCE≌△BCE得∠EDC=∠EBC 由DC∥AB得∠EDC=∠AFD
∴∠AFD=∠EBC
(2)∵DE=EC ∴∠EDC=∠ECD
设∠EDC=∠ECD=∠CBE= x°,则∠CBF=2x°
由BE⊥AF得2x+ x=90° x=30°
∴∠DAB=60°
(3)分两种情况:
①当F在AB延长线上时,∵∠EFB为钝角
∴只能是BE=BF,设∠BEF=∠BFE = x°
可通过三角形内角形为180°得90+ x+ x+ x=180,x=30
∴∠EFB=30°
②当F在线段AB上时,∵∠EFB为钝角
∴只能是FE=FB,设∠BEF=∠EBF= x° ,则有 ∠AFD= 2x°
可证得∠AFD=∠DCE=∠CBE 得x+ 2x=90, x=30 ∴∠EFB=120°
综上:∴∠EFB=30°或120°

练习册系列答案
相关题目