Question

【题目】已知中，，，．点由出发沿向点匀速运动，同时点由出发沿向点匀速运动，它们的速度相同，点在上，，且点在点的下方，当点到达点时，点，也停止运动，连接，设．解答下列问题：

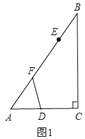
如图，当为何值时，为直角三角形；

如图，把沿翻折，使点落在点．

①当为何值时，四边形为菱形？并求出菱形的面积；

②如图，分别取，的中点，，在整个运动过程中，则线段扫过的区域的形状为________，其面积为________．

Answer 1

【答案】平行四边形

【解析】

（1）△ADF为直角三角形，有两种可能：∠ADF=90°或∠AFD=90°，根据锐角三角函数，分两种情况进行讨论，列方程求解即可；

（2）①根据菱形的判定，可知当AD=DF时，四边形ADFD′为菱形，根据锐角三角函数列方程求出x，计算菱形的面积即可；②根据三角形中位线定理可知，线段MN扫过的区域的形状是平行四边形，其面积为．

解：（1）∵∠ACB=90°，BC=8，tanA=

∴BC=8，AB=10，

∴AD=x，BE=x，AF=6-x，

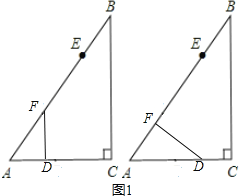
当∠ADF=90°，如图1左图，

∵tanA=

∴cosA=

∴

x=；

当∠AFD=90°，如图1右图，

∵tanA=

∴cosA=

∴

x=，

∴当

x=或x=，

△ADF为直角三角形；

（2）①如图2，

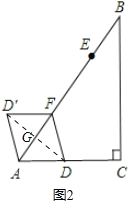
∵AD=AD′，D′F=DF，

∴当AD=DF时，四边形ADFD′为菱形，

∴连接DD′⊥AF于G，AG=，

∵tanA=，

∴cosA=，

∴，

∴x=，

S菱形=×DD′×AF=××=；

②平行四边形，

∵M、N分别为D′F、D′E的中点，

∴MN∥EF，MN=EF=2，

∴线段MN扫过的区域的形状是平行四边形，

当D运动到C，则F正好运动到A，此时MA=D′A=DA=3，

∵∠DAB=∠D′AB，

∴tanA=tan∠D′AB=，

点M到AB的距离设为4x，则（3x）2+（4x）2=32，

解得：x=，

4x=

∴线段MN扫过的区域的形状是平行四边形的面积=2×=．